On standard-errors

It is an euphemism to say that standard-errors are a critical element of your estimations: literally your paper’s results depend on them. It is therefore unfortunate that no conventional “best” way exists to compute them.

For example, when performing the exact same estimation across various software, it is not uncommon to obtain different standard-errors. If your first thought is: there must be a bug… well, put that thought aside because there ain’t no bug. It often boils down to the choices the developer made regarding small sample correction which, maybe surprisingly, has many degrees of freedom when it comes to implementation.

Multiple definitions can create confusion and the purpose of this document is to lay bare the fiddly details of standard-error computation in this package.

The first part of this vignette describes how standard-errors are computed in fixest’s estimations. In particular, it details all the possible choices surrounding small sample correction. Please note that here I don’t discuss the why, but only the how. For a thorough introduction to the topic, see the excellent paper by Zeileis, Koll and Graham (2020). The second part illustrates how to replicate some standard-errors obtained from other estimation methods with fixest.

This document applies to fixest version 0.10.0 or higher.

How standard-errors are computed in `fixest`

There are two components defining the standard-errors in fixest. The main type of standard-error is given by the argument vcov, the small sample correction is defined by the argument ssc.

Here’s an example, the explanations follow in the next two sections:

library(fixest)
data(trade)
# OLS estimation
gravity = feols(log(Euros) ~ log(dist_km) | Destination + Origin + Product + Year, trade)
# Two-way clustered SEs
summary(gravity, vcov = "twoway")

#> OLS estimation, Dep. Var.: log(Euros)
#> Observations: 38,325
#> Fixed-effects: Destination: 15,  Origin: 15,  Product: 20,  Year: 10
#> Standard-errors: Clustered (Destination & Origin) 
#>              Estimate Std. Error  t value   Pr(>|t|)    
#> log(dist_km) -2.16988   0.171367 -12.6621 4.6802e-09 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> RMSE: 1.74337     Adj. R2: 0.705139
#>                 Within R2: 0.219322

# Two-way clustered SEs, without small sample correction
summary(gravity, vcov = "twoway", ssc = ssc(adj = FALSE, cluster.adj = FALSE))

#> OLS estimation, Dep. Var.: log(Euros)
#> Observations: 38,325
#> Fixed-effects: Destination: 15,  Origin: 15,  Product: 20,  Year: 10
#> Standard-errors: Clustered (Destination & Origin) 
#>              Estimate Std. Error  t value   Pr(>|t|)    
#> log(dist_km) -2.16988   0.165494 -13.1115 2.9764e-09 ***
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> RMSE: 1.74337     Adj. R2: 0.705139
#>                 Within R2: 0.219322

The argument `vcov`

The argument vcov can be equal to either: "iid", "hetero", "cluster", "twoway", "NW", "DK", or "conley".

If vcov = "iid", then the standard-errors are based on the assumption that the errors are non correlated and homoskedastic. If vcov = "hetero", this corresponds to the classic hereoskedasticity-robust standard-errors (White correction), where it is assumed that the errors are non correlated but the variance of their generative law may vary.

If vcov = "cluster", then arbitrary correlation of the errors within clusters is accounted for. Same for vcov = "twoway": arbitrary correlation within each of the two clusters is accounted for.

In the context of panel data or time series, vcov = "NW" (Newey-West, 1987) or vcov = "DK" (Driscoll-Kraay, 1998) account for temporal correlation between the errors; the two differing on how to account for heterogeneity between units. Their implementation is based on Millo (2017).

Finally, vcov = "conley" accounts for spatial correlation of the errors.

The argument `ssc`

The type of small sample correction applied is defined by the argument ssc which accepts only objects produced by the function ssc. The main arguments of this function are adj, fixef.K and cluster.adj. I detail each of them below.

Say you have \(\tilde{V}\) the variance-covariance matrix (henceforth VCOV) before any small sample adjustment. Argument adj can be equal to TRUE or FALSE, leading to the following adjustment:

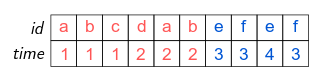
When the estimation contains fixed-effects, the value of \(K\) in the previous adjustment can be determined in different ways, governed by the argument fixef.K. To illustrate how \(K\) is computed, let’s use an example with individual (variable id) and time fixed-effect and with clustered standard-errors. The structure of the 10 observations data is:

The standard-errors are clustered with respect to the cluster variable, further we can see that the variable id is nested within the cluster variable (i.e. each value of id “belongs” to only one value of cluster; e.g. id could represent US counties and cluster US states).

The argument fixef.K can be equal to either "none", "nested" or "full". Then \(K\) will be computed as follows:

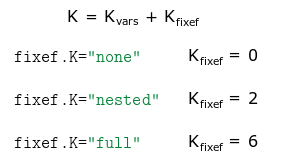
Where \(K_{vars}\) is the number of estimated coefficients associated to the variables. fixef.K="none" discards all fixed-effects coefficients. fixef.K="nested" discards all coefficients that are nested (here the 5 coefficients from id). Finally fixef.K="full" accounts for all fixed-effects coefficients (here 6: equal to 5 from id, plus 2 from time, minus one used as a reference [otherwise collinearity arise]). Note that if fixef.K="nested" and the standard-errors are not clustered, this is equivalent to using fixef.K="full".

The last argument of ssc is cluster.adj. This argument is only relevant when the standard-errors are clustered or when they are corrected for serial correlation (Newey-West or Driscoll-Kraay). Let \(M\) be the sandwich estimator of the VCOV without adjustment. Then for one-way clustered standard errors:

With \(G\) the number of unique elements of the cluster variable (in the previous example \(G=2\) for cluster).

The effect of the adjustment for two-way clustered standard-errors is as follows:

Using the data from the previous example, here the standard-errors are clustered by id and time, leading to \(G_{id}=5\), \(G_{time}=2\), and \(G_{id,time}=10\).

When standard-errors are corrected for serial correlation, the corresponding adjustment applied is \(G_{time} / (G_{time} - 1)\).

Yet more details

You’re already fed up about about these details? I’m sorry but there’s more, so far you’ve only seen the main arguments! I now come to detail three more elements: fixef.force_exact, cluster.df and t.df.

Argument fixef.force_exact is only relevant when there are two or more fixed-effects. By default all the fixed-effects coefficients are accounted for when computing the degrees of freedom. In general this is fine, but in some situations it may overestimate the number of estimated coefficients. Why? Because some of the fixed-effects may be collinear, the effective number of coefficients being lower. Let’s illustrate that with an example. Consider the following set of fixed-effects:

There are 6 different values of id and 4 different values of time. By default, 9 coefficients are used to compute the degrees of freedom (6 plus 4 minus one reference). But we can see here that the “effective” number of coefficients is equal to 8: two coefficients should be removed to avoid collinearity issues (any one from each color set). If you use fixef.force_exact=TRUE, then the function fixef is first run to determine the number of free coefficients in the fixed-effects, this number is then used to compute the degree of freedom.

Argument cluster.df is only relevant when you apply two-way clustering (or higher). It can have two values: either "conventional", or "min" (the default). This affects the adjustments for each clustered matrix. The "conventional" way to make the adjustment has already been described in the previous equation. If cluster.df="min" (again, the default), and for two-way clustered standard errors, the adjustment becomes:

Now instead of having a specific adjustment for each matrix, there is only one adjustment of \(G_{min}/(G_{min}-1)\) where \(G_{min}\) is the minimum cluster size (here \(G_{min}=\min(G_{id},G_{time})\)).

Argument t.df is only relevant when standard-errors are clustered. It affects the way the p-value and confidence intervals are computed. It can be equal to: either "conventional", or "min" (the default). By default, when standard-errors are clustered, the degrees of freedom used in the Student t distribution is equal to the minimum cluster size (among all clusters used to cluster the VCOV) minus one. If t.df="conventional", the degrees of freedom used to find the p-value from the Student t distribution is equal to the number of observations minus the number of estimated coefficients.

Replicating standard-errors from other methods

This section illustrates how the results from fixest compares with the ones from other methods. It also shows how to replicate the latter from fixest.

The data set and heteroskedasticity-robust SEs

Using the Grunfeld data set from the plm package, here are some comparisons when the estimation doesn’t contain fixed-effects.

library(sandwich)
library(plm)

data(Grunfeld)

# Estimations
res_lm    = lm(inv ~ capital, Grunfeld)
res_feols = feols(inv ~ capital, Grunfeld)

# Same standard-errors
rbind(se(res_lm), se(res_feols))

#>      (Intercept)   capital
#> [1,]    15.63927 0.0383394
#> [2,]    15.63927 0.0383394

# Heteroskedasticity-robust covariance
se_lm_hc    = sqrt(diag(vcovHC(res_lm, type = "HC1")))
se_feols_hc = se(res_feols, vcov = "hetero")
rbind(se_lm_hc, se_feols_hc)

#>             (Intercept)    capital
#> se_lm_hc       17.05558 0.06633144
#> se_feols_hc    17.05558 0.06633144

Note that Stata’s reg inv capital, robust also leads to similar results (same SEs, same p-values).

“IID” SEs in the presence of fixed-effects

The most important differences arise in the presence of fixed-effects. Let’s first compare “iid” standard-errors between lm and plm.

# Estimations
est_lm    = lm(inv ~ capital + as.factor(firm) + as.factor(year), Grunfeld)
est_plm   = plm(inv ~ capital + as.factor(year), Grunfeld, index = c("firm", "year"), model = "within")
# we use panel.id so that panel VCOVs can be applied directly
est_feols = feols(inv ~ capital | firm + year, Grunfeld, panel.id = ~firm + year)

#
# "iid" standard-errors
#

# By default fixest clusters the SEs when FEs are present,
#  so we need to ask for iid SEs explicitly.
rbind(se(est_lm)["capital"], se(est_plm)["capital"], se(est_feols, vcov = "iid"))

#>         capital
#> [1,] 0.02597821
#> [2,] 0.02597821
#> [3,] 0.02597821

# p-values:
rbind(pvalue(est_lm)["capital"], pvalue(est_plm)["capital"], pvalue(est_feols, vcov = "iid"))

#>           capital
#> [1,] 1.519204e-35
#> [2,] 1.519204e-35
#> [3,] 1.519204e-35

The standard-errors and p-values are identical, note that this is also the case for Stata’s xtreg.

Clustered SEs

Now for clustered SEs:

# Clustered by firm
se_lm_firm    = se(vcovCL(est_lm, cluster = ~firm, type = "HC1"))["capital"]
se_plm_firm   = se(vcovHC(est_plm, cluster = "group"))["capital"]
se_stata_firm = 0.06328129    # vce(cluster firm)
se_feols_firm = se(est_feols) # By default: clustered according to firm

rbind(se_lm_firm, se_plm_firm, se_stata_firm, se_feols_firm)

#>                  capital
#> se_lm_firm    0.06493478
#> se_plm_firm   0.05693726
#> se_stata_firm 0.06328129
#> se_feols_firm 0.06328129

As we can see, there are three different versions of the standard-errors, feols being identical to Stata’s xtreg clustered SEs. By default, the p-value is also identical to the one from Stata (from fixest version 0.7.0 onwards).

Now let’s see how to replicate the standard-errors from lm and plm:

# How to get the lm version
se_feols_firm_lm = se(est_feols, ssc = ssc(fixef.K = "full"))
rbind(se_lm_firm, se_feols_firm_lm)

#>                     capital
#> se_lm_firm       0.06493478
#> se_feols_firm_lm 0.06493478

# How to get the plm version
se_feols_firm_plm = se(est_feols, ssc = ssc(fixef.K = "none", cluster.adj = FALSE))
rbind(se_plm_firm, se_feols_firm_plm)

#>                      capital
#> se_plm_firm       0.05693726
#> se_feols_firm_plm 0.05693726

HAC SEs

And finally let’s look at Newey-West and Driscoll-Kray standard-errors:

#
# Newey-west
#

se_plm_NW   = se(vcovNW(est_plm))["capital"]
se_feols_NW = se(est_feols, vcov = "NW")

rbind(se_plm_NW, se_feols_NW)

#>                capital
#> se_plm_NW   0.08390222
#> se_feols_NW 0.08629896

# we can replicate plm's by changing the type of SSC:
rbind(se_plm_NW, 
      se(est_feols, vcov = NW ~ ssc(adj = FALSE, cluster.adj = FALSE)))

#>              capital
#> se_plm_NW 0.08390222
#>           0.08390222

#
# Driscoll-Kraay
#

se_plm_DK   = se(vcovSCC(est_plm))["capital"]
se_feols_DK = se(est_feols, vcov = "DK")

rbind(se_plm_DK, se_feols_DK)

#>                capital
#> se_plm_DK   0.08359734
#> se_feols_DK 0.08800884

# Replicating plm's
rbind(se_plm_DK, 
      se(est_feols, vcov = DK ~ ssc(adj = FALSE, cluster.adj = FALSE)))

#>              capital
#> se_plm_DK 0.08359734
#>           0.08359734

As we can see, the type of small sample correction we choose can have a non-negligible impact on the standard-error.

Other multiple fixed-effects methods

Now a specific comparison with lfe (version 2.8-7) and Stata’s reghdfe which are popular tools to estimate econometric models with multiple fixed-effects.

From fixest version 0.7.0 onwards, the standard-errors and p-values are computed similarly to reghdfe, for both clustered and multiway clustered standard errors. So the comparison here focuses on lfe.

Here are the differences and similarities with lfe:

library(lfe)

# lfe: clustered by firm
est_lfe = felm(inv ~ capital | firm + year | 0 | firm, Grunfeld)
se_lfe_firm = se(est_lfe)

# The two are different, and it cannot be directly replicated by feols
rbind(se_lfe_firm, se_feols_firm)

#>                  capital
#> se_lfe_firm   0.06016851
#> se_feols_firm 0.06328129

# You have to provide a custom VCOV to replicate lfe's VCOV
my_vcov = vcov(est_feols, ssc = ssc(adj = FALSE))
se(est_feols, vcov = my_vcov * 199/198) # Note that there are 200 observations

#>    capital 
#> 0.06016851

# Differently from feols, the SEs in lfe are different if year is not a FE:
# => now SEs are identical.
rbind(se(felm(inv ~ capital + factor(year) | firm | 0 | firm, Grunfeld))["capital"],
      se(feols(inv ~ capital + factor(year) | firm, Grunfeld))["capital"])

#>         capital
#> [1,] 0.06328129
#> [2,] 0.06328129

# Now with two-way clustered standard-errors
est_lfe_2way  = felm(inv ~ capital | firm + year | 0 | firm + year, Grunfeld)
se_lfe_2way   = se(est_lfe_2way)
se_feols_2way = se(est_feols, vcov = "twoway")
rbind(se_lfe_2way, se_feols_2way)

#>                  capital
#> se_lfe_2way   0.06213837
#> se_feols_2way 0.06041290

# To obtain the same SEs, use cluster.df = "conventional"
sum_feols_2way_conv = summary(est_feols, vcov = twoway ~ ssc(cluster.df = "conv"))
rbind(se_lfe_2way, se(sum_feols_2way_conv))

#>                capital
#> se_lfe_2way 0.06213837
#>             0.06213837

# We also obtain the same p-values
rbind(pvalue(est_lfe_2way), pvalue(sum_feols_2way_conv))

#>           capital
#> [1,] 9.273982e-05
#> [2,] 9.273982e-05

As we can see, there is only slight differences with lfe when computing clustered standard-errors. For multiway clustered standard-errors, it is easy to replicate the way lfe computes them.

Defining how to compute the standard-errors once and for all

Once you’ve found the preferred way to compute the standard-errors for your current project, you can set it permanently using the functions setFixest_ssc() and setFixest_vcov().

For example, if you want to remove the small sample adjustment, just use:

setFixest_ssc(ssc(adj = FALSE))

By default, the standard-errors are clustered in the presence of fixed-effects and in the presence of a panel. You can change this behavior with, e.g.:

setFixest_vcov(no_FE = "iid", one_FE = "iid", 
               two_FE = "hetero", panel = "driscoll_kraay")

which changes the way the default standard-errors are computed when the estimation contains no fixed-effects, one fixed-effect, two or more fixed-effects, or is a panel.

Changelog

Version 0.10.0 brings about many important changes:
- The arguments se and cluster have been replaced by the argument vcov. Retro compatibility is ensured.
- The argument dof has been renamed to ssc for clarity (since it was dealing with small sample correction). This is not retro compatible.
- Three new types of standard-errors are added: Newey-West and Driscoll-Kraay for panel data; Conley to account for spatial correlation.
- The argument ssc can now be directly summoned in the vcov formula.
- The functions setFixest_dof and setFixest_se have been renamed into setFixest_ssc and setFixest_vcov. Retro compatibility is not ensured.
- The default standard-error name has changed from "standard" to "iid" (thanks to Grant McDermott for the suggestion!).
- Since lfe has returned to CRAN (good news!), the code chunks involving it are now re-evaluated.
- The illustration is now based on the Grunfeld data set from the plm package (to avoid problems with RNG).
Version 0.8.0. Evaluation of the chunks related to lfe have been removed since its archival on the CRAN. Hard values from the last CRAN version are maintained.
Version 0.7.0 introduces the following important modifications:
- To increase clarity, se = "white" becomes se = "hetero". Retro-compatibility is ensured.
- The default values for computing clustered standard-errors become similar to reghdfe to avoid cross-software confusion. That is, now by default cluster.df = "min" and t.df = "min" (whereas in the previous version it was cluster.df = "conventional" and t.df = "conventional").

References & acknowledgments

I wish to thank Karl Dunkle Werner, Grant McDermott and Ivo Welch for raising the issue and for helpful discussions. Any error is of course my own.

Cameron AC, Gelbach JB, Miller DL (2011). “Robust Inference with Multiway Clustering”, Journal of Business & Ecomomic Statistics, 29(2), 238–249.

Kauermann G, Carroll RJ (2001). “A Note on the Efficiency of Sandwich Covariance Matrix Estimation”, Journal of the American Statistical Association, 96(456), 1387–1396.

MacKinnon JG, White H (1985). “Some heteroskedasticity-consistent covariance matrix estimators with improved finite sample properties” Journal of Econometrics, 29(3), 305–325.

Millo G (2017). “Robust Standard Error Estimators for Panel Models: A Unifying Approach” Journal of Statistical Software, 82(3).

Zeileis A, Koll S, Graham N (2020). “Various Versatile Variances: An Object-Oriented Implementation of Clustered Covariances in R” Journal of Statistical Software, 95(1), 1–36.

Laurent Berge

2024-06-11

How standard-errors are computed in `fixest`

The argument `vcov`

The argument `ssc`

Yet more details

Replicating standard-errors from other methods

The data set and heteroskedasticity-robust SEs

“IID” SEs in the presence of fixed-effects

Clustered SEs

HAC SEs

Other multiple fixed-effects methods

Defining how to compute the standard-errors once and for all

Changelog

References & acknowledgments

On standard-errors

Laurent Berge

2024-06-11

How standard-errors are computed in fixest

The argument vcov

The argument ssc

Yet more details

Replicating standard-errors from other methods

The data set and heteroskedasticity-robust SEs

“IID” SEs in the presence of fixed-effects

Clustered SEs

HAC SEs

Other multiple fixed-effects methods

Defining how to compute the standard-errors once and for all

Changelog

References & acknowledgments

How standard-errors are computed in `fixest`

The argument `vcov`

The argument `ssc`