This function plots the results of estimations (coefficients and confidence intervals).
The function iplot restricts the output to variables created with i, either
interactions with factors or raw factors.
Usage
coefplot(
...,
objects = NULL,
style = NULL,
se,
ci_low,
ci_high,
df.t = NULL,
vcov = NULL,
cluster = NULL,
x,
x.shift = 0,
horiz = FALSE,
dict = NULL,
keep,
drop,
order,
ci.width = "1%",
ci_level = 0.95,
add = FALSE,
plot_prms = list(),
pch = c(20, 17, 15, 21, 24, 22),
col = 1:8,
cex = 1,
lty = 1,
lwd = 1,
ylim = NULL,
xlim = NULL,
pt.pch = pch,
pt.bg = NULL,
pt.cex = cex,
pt.col = col,
ci.col = col,
pt.lwd = lwd,
ci.lwd = lwd,
ci.lty = lty,
grid = TRUE,
grid.par = list(lty = 3, col = "gray"),
zero = TRUE,
zero.par = list(col = "black", lwd = 1),
pt.join = FALSE,
pt.join.par = list(col = pt.col, lwd = lwd),
ci.join = FALSE,
ci.join.par = list(lwd = lwd, col = col, lty = 2),
ci.fill = FALSE,
ci.fill.par = list(col = "lightgray", alpha = 0.5),
ref = "auto",
ref.line = "auto",
ref.line.par = list(col = "black", lty = 2),
lab.cex,
lab.min.cex = 0.85,
lab.max.mar = 0.25,
lab.fit = "auto",
xlim.add,
ylim.add,
only.params = FALSE,
sep,
as.multiple = FALSE,
bg,
group = "auto",
group.par = list(lwd = 2, line = 3, tcl = 0.75),
main = "Effect on __depvar__",
value.lab = "Estimate and __ci__ Conf. Int.",
ylab = NULL,
xlab = NULL,
sub = NULL,
i.select = NULL,
do_iplot = NULL
)
iplot(
...,
i.select = 1,
objects = NULL,
style = NULL,
se,
ci_low,
ci_high,
df.t = NULL,
vcov = NULL,
cluster = NULL,
x,
x.shift = 0,
horiz = FALSE,
dict = NULL,
keep,
drop,
order,
ci.width = "1%",
ci_level = 0.95,
add = FALSE,
plot_prms = list(),
pch = c(20, 17, 15, 21, 24, 22),
col = 1:8,
cex = 1,
lty = 1,
lwd = 1,
ylim = NULL,
xlim = NULL,
pt.pch = pch,
pt.bg = NULL,
pt.cex = cex,
pt.col = col,
ci.col = col,
pt.lwd = lwd,
ci.lwd = lwd,
ci.lty = lty,
grid = TRUE,
grid.par = list(lty = 3, col = "gray"),
zero = TRUE,
zero.par = list(col = "black", lwd = 1),
pt.join = FALSE,
pt.join.par = list(col = pt.col, lwd = lwd),
ci.join = FALSE,
ci.join.par = list(lwd = lwd, col = col, lty = 2),
ci.fill = FALSE,
ci.fill.par = list(col = "lightgray", alpha = 0.5),
ref = "auto",
ref.line = "auto",
ref.line.par = list(col = "black", lty = 2),
lab.cex,
lab.min.cex = 0.85,
lab.max.mar = 0.25,
lab.fit = "auto",
xlim.add,
ylim.add,
only.params = FALSE,
sep,
as.multiple = FALSE,
bg,
group = "auto",
group.par = list(lwd = 2, line = 3, tcl = 0.75),
main = "Effect on __depvar__",
value.lab = "Estimate and __ci__ Conf. Int.",
ylab = NULL,
xlab = NULL,
sub = NULL
)Arguments
- ...
Other arguments to be passed to
summary, ifobjectis an estimation, and/or to the functionplotorlines(ifadd = TRUE).- objects
A list of
fixestestimation objects, orNULL(default). If provided, the objects in...are ignored and the only coefficients reported are the ones in the argumentobjects. #' @param vcov Versatile argument to specify the VCOV. In general, it is either a character scalar equal to a VCOV type, either a formula of the form: vcov_type ~ variables. The VCOV types implemented are: "iid", "hetero" (or "HC1"), "cluster", "twoway", "NW" (or "newey_west"), "DK" (or "driscoll_kraay"), and "conley". It also accepts object from vcov_cluster, vcov_NW, NW, vcov_DK, DK, vcov_conley and conley. It also accepts covariance matrices computed externally. Finally it accepts functions to compute the covariances. See the vcov documentation in the vignette. You can pass several VCOVs (as above) if you nest them into a list. If the number of VCOVs equals the number of models, eahc VCOV is mapped to the appropriate model. If there is one model and several VCOVs, or if the first element of the list is equal to"each"or"times", then the estimations will be replicated and the results for each estimation and each VCOV will be reported.- style
A character scalar giving the style of the plot to be used. You can set styles with the function
setFixest_coefplot, setting all the default values of the function. If missing, then it switches to either "default" or "iplot", depending on the calling function.- se
The standard errors of the estimates. It may be missing.
- ci_low
If
seis not provided, the lower bound of the confidence interval. For each estimate.- ci_high
If
seis not provided, the upper bound of the confidence interval. For each estimate.- df.t
Integer scalar or
NULL(default). The degrees of freedom (DoF) to use when computing the confidence intervals with the Student t. By default it tries to capture the DoF from the estimation. To use a Normal law to compute the confidence interval, usedf.t = Inf.- vcov
Versatile argument to specify the VCOV. In general, it is either a character scalar equal to a VCOV type, either a formula of the form: vcov_type ~ variables. The VCOV types implemented are: "iid", "hetero" (or "HC1"), "cluster", "twoway", "NW" (or "newey_west"), "DK" (or "driscoll_kraay"), and "conley". It also accepts object from vcov_cluster, vcov_NW, NW, vcov_DK, DK, vcov_conley and conley. It also accepts covariance matrices computed externally. Finally it accepts functions to compute the covariances. See the vcov documentation in the vignette. You can pass several VCOVs (as above) if you nest them into a list. If the number of VCOVs equals the number of models, eahc VCOV is mapped to the appropriate model. If there is one model and several VCOVs, or if the first element of the list is equal to
"each"or"times", then the estimations will be replicated and the results for each estimation and each VCOV will be reported.- cluster
Tells how to cluster the standard-errors (if clustering is requested). Can be either a list of vectors, a character vector of variable names, a formula or an integer vector. Assume we want to perform 2-way clustering over
var1andvar2contained in the data.framebaseused for the estimation. All the followingclusterarguments are valid and do the same thing:cluster = base[, c("var1", "var2")],cluster = c("var1", "var2"),cluster = ~var1+var2. If the two variables were used as fixed-effects in the estimation, you can leave it blank withvcov = "twoway"(assumingvar1[resp.var2] was the 1st [resp. 2nd] fixed-effect). You can interact two variables using^with the following syntax:cluster = ~var1^var2orcluster = "var1^var2".- x
The value of the x-axis. If missing, the names of the argument
estimateare used.- x.shift
Shifts the confidence intervals bars to the left or right, depending on the value of
x.shift. Default is 0.- horiz
A logical scalar, default is
FALSE. Whether to display the confidence intervals horizontally instead of vertically.- dict
A named character vector or a logical scalar. It changes the original variable names to the ones contained in the
dictionary. E.g. to change the variables namedaandb3to (resp.) “$log(a)$” and to “$bonus^3$”, usedict=c(a="$log(a)$",b3="$bonus^3$"). By default, it is equal togetFixest_dict(), a default dictionary which can be set withsetFixest_dict. You can usedict = FALSEto disable it. By defaultdictmodifies the entries in the global dictionary, to disable this behavior, use "reset" as the first element (ex:dict=c("reset", mpg="Miles per gallon")).- keep
Character vector. This element is used to display only a subset of variables. This should be a vector of regular expressions (see
base::regexhelp for more info). Each variable satisfying any of the regular expressions will be kept. This argument is applied post aliasing (see argumentdict). Example: you have the variablex1tox55and want to display onlyx1tox9, then you could usekeep = "x[[:digit:]]$". If the first character is an exclamation mark, the effect is reversed (e.g. keep = "!Intercept" means: every variable that does not contain “Intercept” is kept). See details.- drop
Character vector. This element is used if some variables are not to be displayed. This should be a vector of regular expressions (see
base::regexhelp for more info). Each variable satisfying any of the regular expressions will be discarded. This argument is applied post aliasing (see argumentdict). Example: you have the variablex1tox55and want to display onlyx1tox9, then you could usedrop = "x[[:digit:]]{2}". If the first character is an exclamation mark, the effect is reversed (e.g. drop = "!Intercept" means: every variable that does not contain “Intercept” is dropped). See details.- order
Character vector. This element is used if the user wants the variables to be ordered in a certain way. This should be a vector of regular expressions (see
base::regexhelp for more info). The variables satisfying the first regular expression will be placed first, then the order follows the sequence of regular expressions. This argument is applied post aliasing (see argumentdict). Example: you have the following variables:month1tomonth6, thenx1tox5, thenyear1toyear6. If you want to display first the x's, then the years, then the months you could use:order = c("x", "year"). If the first character is an exclamation mark, the effect is reversed (e.g. order = "!Intercept" means: every variable that does not contain “Intercept” goes first). See details.- ci.width
The width of the extremities of the confidence intervals. Default is
0.1.- ci_level
Scalar between 0 and 1: the level of the CI. By default it is equal to 0.95.
- add
Default is
FALSE, if the intervals are to be added to an existing graph. Note that if it is the case, then the argumentxMUST be numeric.- plot_prms
A named list. It may contain additionnal parameters to be passed to the plot.
- pch
The patch of the coefficient estimates. Default is 1 (circle). This is an alias to tha argument
pt.pch.- col
The color of the points and the confidence intervals. Default is 1 ("black"). Note that you can set the colors separately for each of them with
pt.colandci.col.- cex
Numeric, default is 1. Expansion factor for the points
- lty
The line type of the confidence intervals. Default is 1. This is an alias to the argument
ci.lty.- lwd
General line with. Default is 1.
- ylim
Numeric vector of length 2 which gives the limits of the plotting region for the y-axis. The default is
NULL, which means that it is automatically defined. Use the argumentylim.addto simply increase or decrese the default limits.- xlim
Numeric vector of length 2 which gives the limits of the plotting region for the x-axis. The default is
NULL, which means that it is automatically defined. Use the argumentxlim.addto simply increase or decrese the default limits.- pt.pch
The patch of the coefficient estimates. Default is 1 (circle).
- pt.bg
The background color of the point estimate (when the
pt.pchis in 21 to 25). Defaults to NULL.- pt.cex
The size of the coefficient estimates. Default is the other argument
cex.- pt.col
The color of the coefficient estimates. Default is equal to the argument
col.- ci.col
The color of the confidence intervals. Default is equal to the argument
col.- pt.lwd
The line width of the coefficient estimates. Default is equal to the other argument
lwd.- ci.lwd
The line width of the confidence intervals. Default is equal to the other argument
lwd.- ci.lty
The line type of the confidence intervals. Default is 1.
- grid
Logical, default is
TRUE. Whether a grid should be displayed. You can set the display of the grid with the argumentgrid.par.- grid.par
List. Parameters of the grid. The default values are:
lty = 3andcol = "gray". You can add any graphical parameter that will be passed tographics::abline. You also have two additional arguments: usehoriz = FALSEto disable the horizontal lines, and usevert = FALSEto disable the vertical lines. Eg:grid.par = list(vert = FALSE, col = "red", lwd = 2).- zero
Logical, default is
TRUE. Whether the 0-line should be emphasized. You can set the parameters of that line with the argumentzero.par.- zero.par
List. Parameters of the zero-line. The default values are
col = "black"andlwd = 1. You can add any graphical parameter that will be passed tographics::abline. Example:zero.par = list(col = "darkblue", lwd = 3).- pt.join
Logical, default is
FALSE. IfTRUE, then the coefficient estimates are joined with a line.- pt.join.par
List. Parameters of the line joining the coefficients. The default values are:
col = pt.colandlwd = lwd. You can add any graphical parameter that will be passed tolines. Eg:pt.join.par = list(lty = 2).- ci.join
Logical default to
FALSE. Whether to join the extremities of the confidence intervals. IfTRUE, then you can set the graphical parameters with the argumentci.join.par.- ci.join.par
A list of parameters to be passed to
graphics::lines. Only used ifci.join=TRUE. By default it is equal tolist(lwd = lwd, col = col, lty = 2).- ci.fill
Logical default to
FALSE. Whether to fill the confidence intervals with a color. IfTRUE, then you can set the graphical parameters with the argumentci.fill.par.- ci.fill.par
A list of parameters to be passed to
graphics::polygon. Only used ifci.fill=TRUE. By default it is equal tolist(col = "lightgray", alpha = 0.5). Note thatalphais a special parameter that adds transparency to the color (ranges from 0 to 1).- ref
Used to add points at
y = 0(typically to visualize reference points). Either: i) "auto" (default), ii) a character vector of length 1, iii) a list of length 1, iv) a named integer vector of length 1, or v) a numeric vector. By default, iniplot, if the argumentrefhas been used in the estimation, these references are automatically added. If ii), ie a character scalar, then that coefficient equal to zero is added as the first coefficient. If a list or a named integer vector of length 1, then the integer gives the position of the reference among the coefficients and the name gives the coefficient name. A non-named numeric value ofrefonly works if the x-axis is also numeric (which can happen iniplot).- ref.line
Logical or numeric, default is "auto", whose behavior depends on the situation. It is
TRUEonly if: i) interactions are plotted, ii) the x values are numeric and iii) a reference is found. IfTRUE, then a vertical line is drawn at the level of the reference value. Otherwise, if numeric a vertical line will be drawn at that specific value.- ref.line.par
List. Parameters of the vertical line on the reference. The default values are:
col = "black"andlty = 2. You can add any graphical parameter that will be passed tographics::abline. Eg:ref.line.par = list(lty = 1, lwd = 3).- lab.cex
The size of the labels of the coefficients. Default is missing. It is automatically set by an internal algorithm which can go as low as
lab.min.cex(another argument).- lab.min.cex
The minimum size of the coefficients labels, as set by the internal algorithm. Default is 0.85.
- lab.max.mar
The maximum size the left margin can take when trying to fit the coefficient labels into it (only when
horiz = TRUE). This is used in the internal algorithm fitting the coefficient labels. Default is0.25.- lab.fit
The method to fit the coefficient labels into the plotting region (only when
horiz = FALSE). Can be"auto"(the default),"simple","multi"or"tilted". If"simple", then the classic axis is drawn. If"multi", then the coefficient labels are fit horizontally across several lines, such that they don't collide. If"tilted", then the labels are tilted. If"auto", an automatic choice between the three is made.- xlim.add
A numeric vector of length 1 or 2. It represents an extension factor of xlim, in percentage. Eg:
xlim.add = c(0, 0.5)extendsxlimof 50% on the right. If of length 1, positive values represent the right, and negative values the left (Eg:xlim.add = -0.5is equivalent toxlim.add = c(0.5, 0)).- ylim.add
A numeric vector of length 1 or 2. It represents an extension factor of ylim, in percentage. Eg:
ylim.add = c(0, 0.5)extendsylimof 50% on the top. If of length 1, positive values represent the top, and negative values the bottom (Eg:ylim.add = -0.5is equivalent toylim.add = c(0.5, 0)).- only.params
Logical, default is
FALSE. IfTRUEno graphic is displayed, only the values ofxandyused in the plot are returned.- sep
The distance between two estimates – only when argument
objectis a list of estimation results.- as.multiple
Logical: default is
FALSE. Only whenobjectis a single estimation result: whether each coefficient should have a different color, line type, etc. By default they all get the same style.- bg
Background color for the plot. By default it is white.
- group
A list, default is missing. Each element of the list reports the coefficients to be grouped while the name of the element is the group name. Each element of the list can be either: i) a character vector of length 1, ii) of length 2, or ii) a numeric vector. If equal to: i) then it is interpreted as a pattern: all element fitting the regular expression will be grouped (note that you can use the special character "^^" to clean the beginning of the names, see example), if ii) it corresponds to the first and last elements to be grouped, if iii) it corresponds to the coefficients numbers to be grouped. If equal to a character vector, you can use a percentage to tell the algorithm to look at the coefficients before aliasing (e.g.
"%varname"). Example of valid uses:group=list(group_name=\"pattern\"),group=list(group_name=c(\"var_start\", \"var_end\")),group=list(group_name=1:2)). See details.- group.par
A list of parameters controlling the display of the group. The parameters controlling the line are:
lwd,tcl(length of the tick),line.adj(adjustment of the position, default is 0),tick(whether to add the ticks),lwd.ticks,col.ticks. Then the parameters controlling the text:text.adj(adjustment of the position, default is 0),text.cex,text.font,text.col.- main
The title of the plot. Default is
"Effect on __depvar__". You can use the special variable__depvar__to set the title (useful when you set the plot default withsetFixest_coefplot).- value.lab
The label to appear on the side of the coefficient values. If
horiz = FALSE, the label appears in the y-axis. Ifhoriz = TRUE, then it appears on the x-axis. The default is equal to"Estimate and __ci__ Conf. Int.", with__ci__a special variable giving the value of the confidence interval.- ylab
The label of the y-axis, default is
NULL. Note that ifhoriz = FALSE, it overrides the value of the argumentvalue.lab.- xlab
The label of the x-axis, default is
NULL. Note that ifhoriz = TRUE, it overrides the value of the argumentvalue.lab.- sub
A subtitle, default is
NULL.- i.select
Integer scalar, default is 1. In
iplot, used to select which variable created withi()to select. Only used when there are several variables created withi. This is an index, just try increasing numbers to hopefully obtain what you want. Note that it works much better when the variables are "pure"i()and not interacted with other variables. For example:i(species, x1)is good whilei(species):x1isn't. The latter will also work but the index may feel weird in case there are manyi()variables.- do_iplot
Logical, default is
FALSE. For internal use only. IfTRUE, theniplotis run instead ofcoefplot.
Setting custom default values
The function coefplot dispose of many arguments to parametrize the plots. Most
of these arguments can be set once an for all using the function setFixest_coefplot.
See Example 3 below for a demonstration.
iplot
The function iplot restricts coefplot to interactions or factors created
with the function i. Only one of the i-variables will be plotted at a time.
If you have several i-variables, you can navigate through them with the i.select argument.
The argument i.select is an index that will go through all the i-variables.
It will work well if the variables are pure, meaning not interacted with other
variables. If the i-variables are interacted, the index may have an odd behavior
but will (in most cases) work all the same, just try some numbers up until you
(hopefully) obtain the graph you want.
Note, importantly, that interactions of two factor variables are (in general) disregarded since they would require a 3-D plot to be properly represented.
Arguments keep, drop and order
The arguments keep, drop and order use regular expressions. If you are not aware
of regular expressions, I urge you to learn it, since it is an extremely powerful way
to manipulate character strings (and it exists across most programming languages).
For example drop = "Wind" would drop any variable whose name contains "Wind". Note that
variables such as "Temp:Wind" or "StrongWind" do contain "Wind", so would be dropped.
To drop only the variable named "Wind", you need to use
drop = "^Wind$" (with "^" meaning beginning, resp. "$" meaning end,
of the string => this is the language of regular expressions).
Although you can combine several regular expressions in a single character
string using pipes, drop also accepts a vector of regular expressions.
You can use the special character "!" (exclamation mark) to reverse the effect
of the regular expression (this feature is specific to this function).
For example drop = "!Wind" would drop any variable that does not contain "Wind".
You can use the special character "%" (percentage) to make reference to the
original variable name instead of the aliased name. For example, you have a
variable named "Month6", and use a dictionary dict = c(Month6="June").
Thus the variable will be displayed as "June".
If you want to delete that variable, you can use either drop="June",
or drop="%Month6" (which makes reference to its original name).
The argument order takes in a vector of regular expressions, the order will follow the
elements of this vector. The vector gives a list of priorities,
on the left the elements with highest priority.
For example, order = c("Wind", "!Inter", "!Temp") would give highest priorities to
the variables containing "Wind" (which would then appear first),
second highest priority is the variables not containing "Inter", last,
with lowest priority, the variables not containing "Temp".
If you had the following variables: (Intercept), Temp:Wind, Wind, Temp you
would end up with the following order: Wind, Temp:Wind, Temp, (Intercept).
See also
See setFixest_coefplot to set the default values of coefplot, and the estimation
functions: e.g. feols, fepois, feglm, fenegbin.
Examples
#
# Example 1: Stacking two sets of results on the same graph
#
# Estimation on Iris data with one fixed-effect (Species)
# + we cluster the standard-errors
est = feols(Petal.Length ~ Petal.Width + Sepal.Width | Species,
iris, vcov = "cluster")
# Now with "regular" standard-errors
est_std = summary(est, vcov = "iid")
# You can plot the two results at once
coefplot(est, est_std)
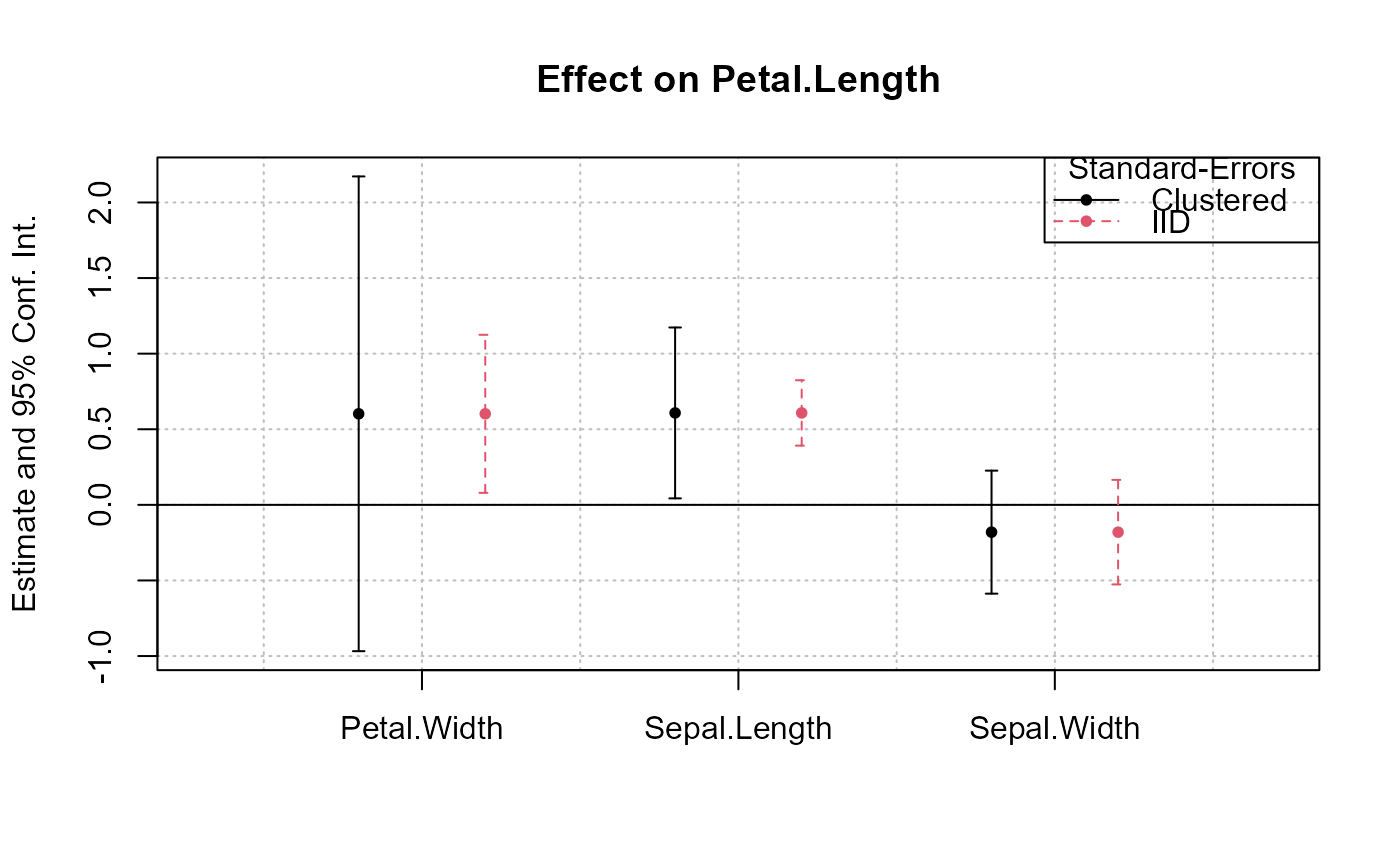
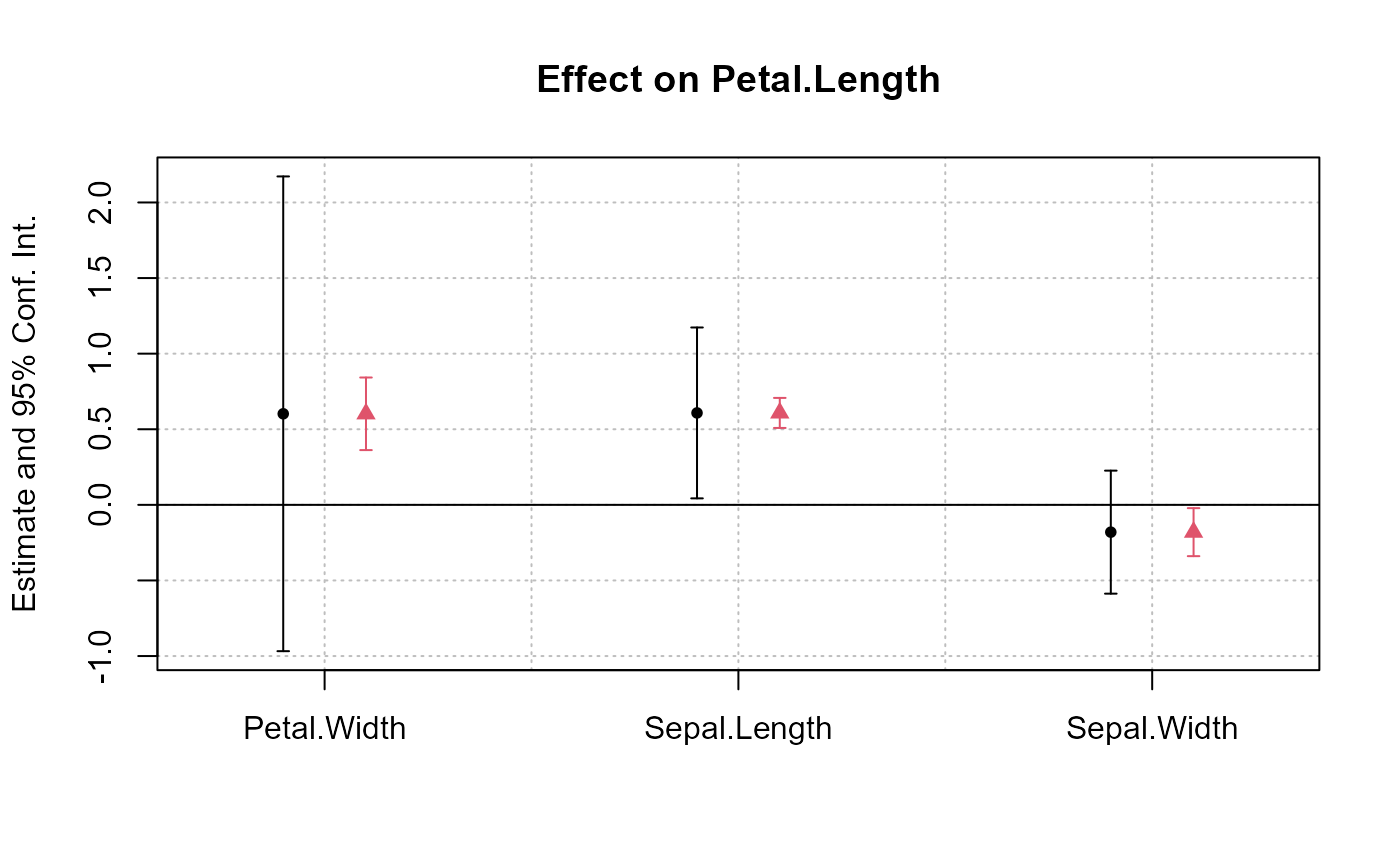 # You could also use the argument vcov
coefplot(est, vcov = list("cluster", "iid"))
# Alternatively, you can use the argument x.shift
# to do it sequentially:
# First graph with clustered standard-errors
coefplot(est, x.shift = -.2)
# 'x.shift' was used to shift the coefficients to the left.
# Second set of results: this time with
# standard-errors that are not clustered.
coefplot(est, vcov = "iid", x.shift = .2,
add = TRUE, col = 2, ci.lty = 2, pch = 15)
legend("topright", col = 1:2, pch = 20, lwd = 1, lty = 1:2,
legend = c("Clustered", "IID"), title = "Standard-Errors")
# You could also use the argument vcov
coefplot(est, vcov = list("cluster", "iid"))
# Alternatively, you can use the argument x.shift
# to do it sequentially:
# First graph with clustered standard-errors
coefplot(est, x.shift = -.2)
# 'x.shift' was used to shift the coefficients to the left.
# Second set of results: this time with
# standard-errors that are not clustered.
coefplot(est, vcov = "iid", x.shift = .2,
add = TRUE, col = 2, ci.lty = 2, pch = 15)
legend("topright", col = 1:2, pch = 20, lwd = 1, lty = 1:2,
legend = c("Clustered", "IID"), title = "Standard-Errors")
 #
# Example 2: Interactions
#
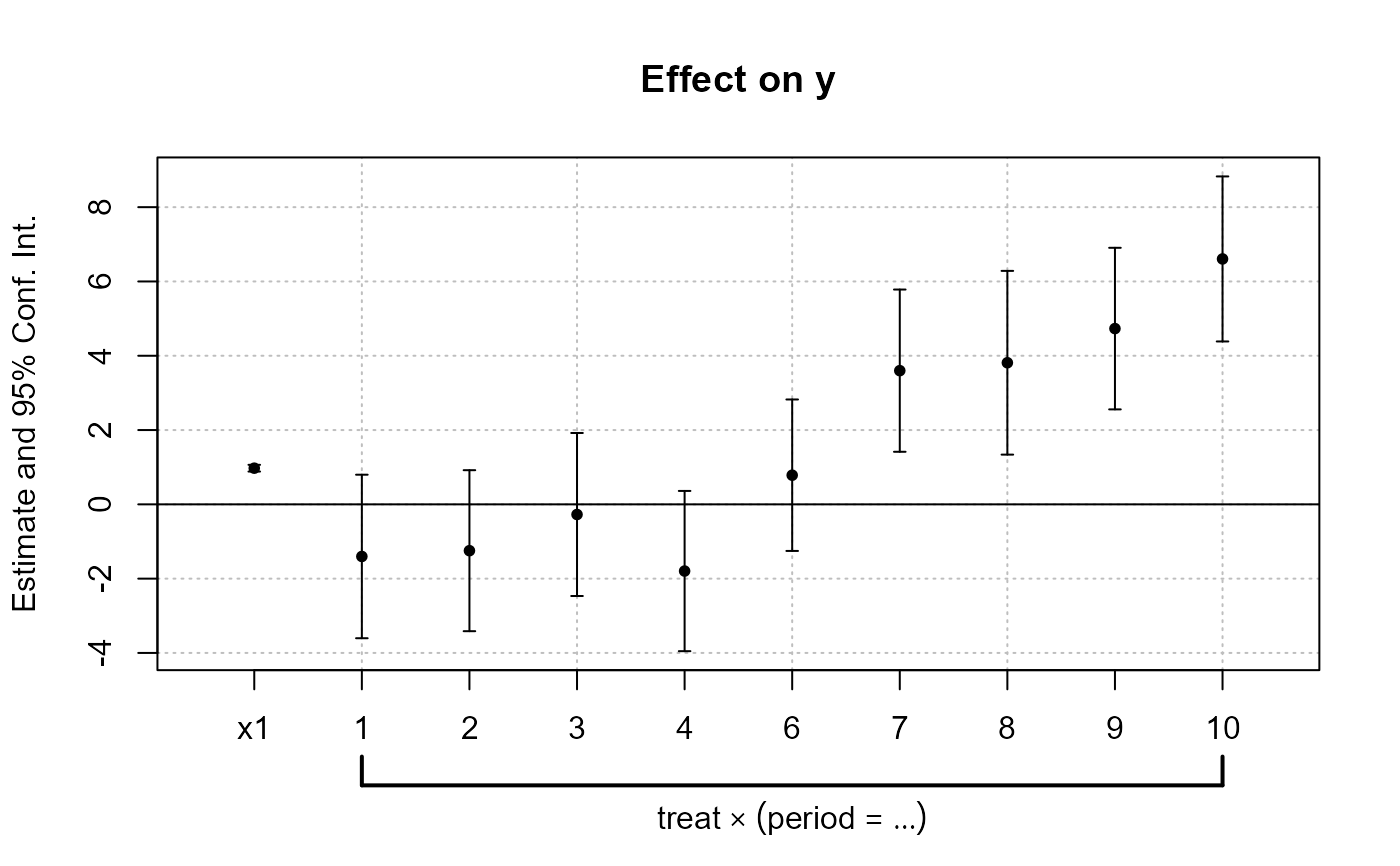
# Now we estimate and plot the "yearly" treatment effects
data(base_did)
base_inter = base_did
# We interact the variable 'period' with the variable 'treat'
est_did = feols(y ~ x1 + i(period, treat, 5) | id + period, base_inter)
# In the estimation, the variable treat is interacted
# with each value of period but 5, set as a reference
# coefplot will show all the coefficients:
coefplot(est_did)
#
# Example 2: Interactions
#
# Now we estimate and plot the "yearly" treatment effects
data(base_did)
base_inter = base_did
# We interact the variable 'period' with the variable 'treat'
est_did = feols(y ~ x1 + i(period, treat, 5) | id + period, base_inter)
# In the estimation, the variable treat is interacted
# with each value of period but 5, set as a reference
# coefplot will show all the coefficients:
coefplot(est_did)
 # Note that the grouping of the coefficients is due to 'group = "auto"'
# If you want to keep only the coefficients
# created with i() (ie the interactions), use iplot
iplot(est_did)
# Note that the grouping of the coefficients is due to 'group = "auto"'
# If you want to keep only the coefficients
# created with i() (ie the interactions), use iplot
iplot(est_did)
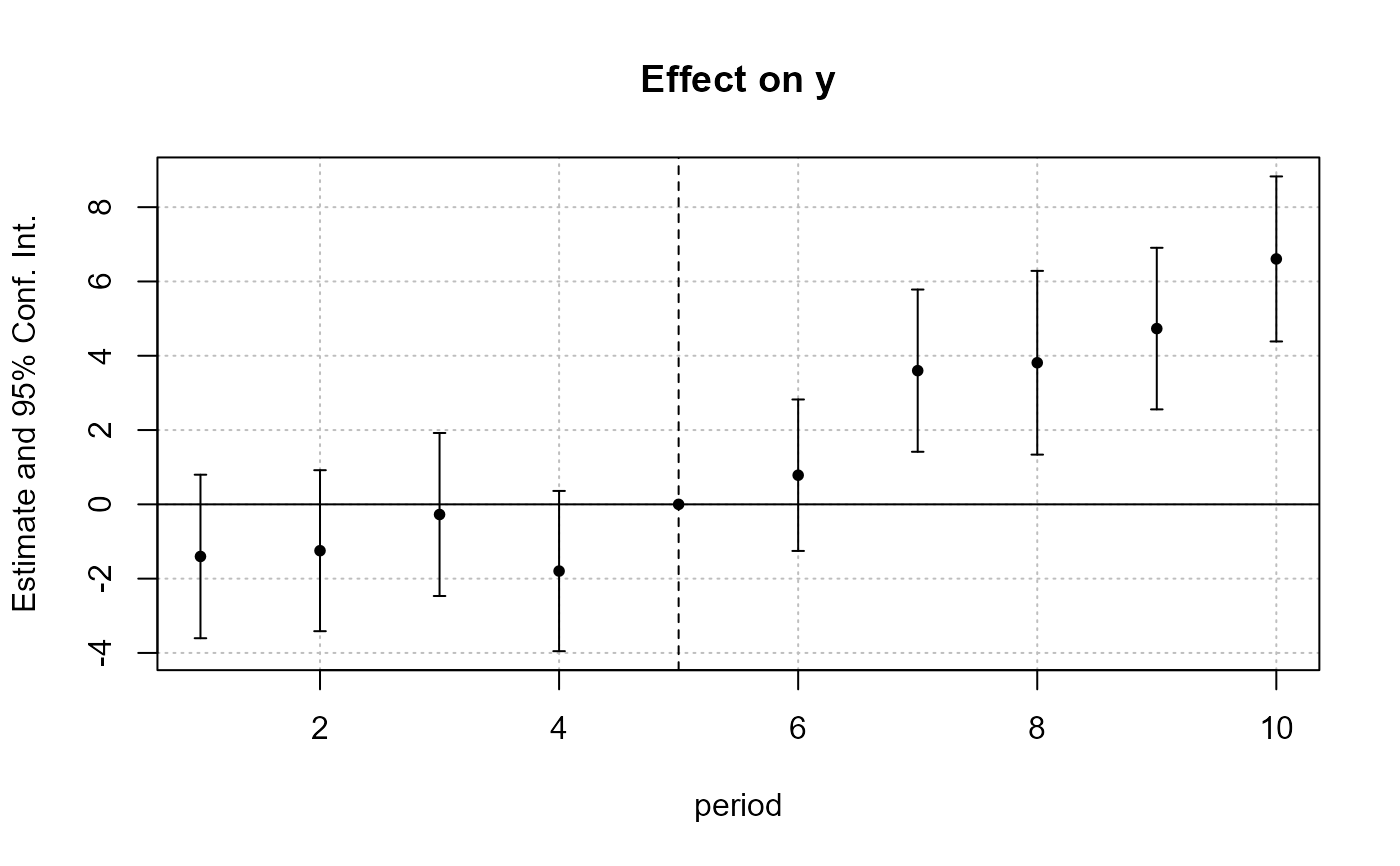 # We can see that the graph is different from before:
# - only interactions are shown,
# - the reference is present,
# => this is fully flexible
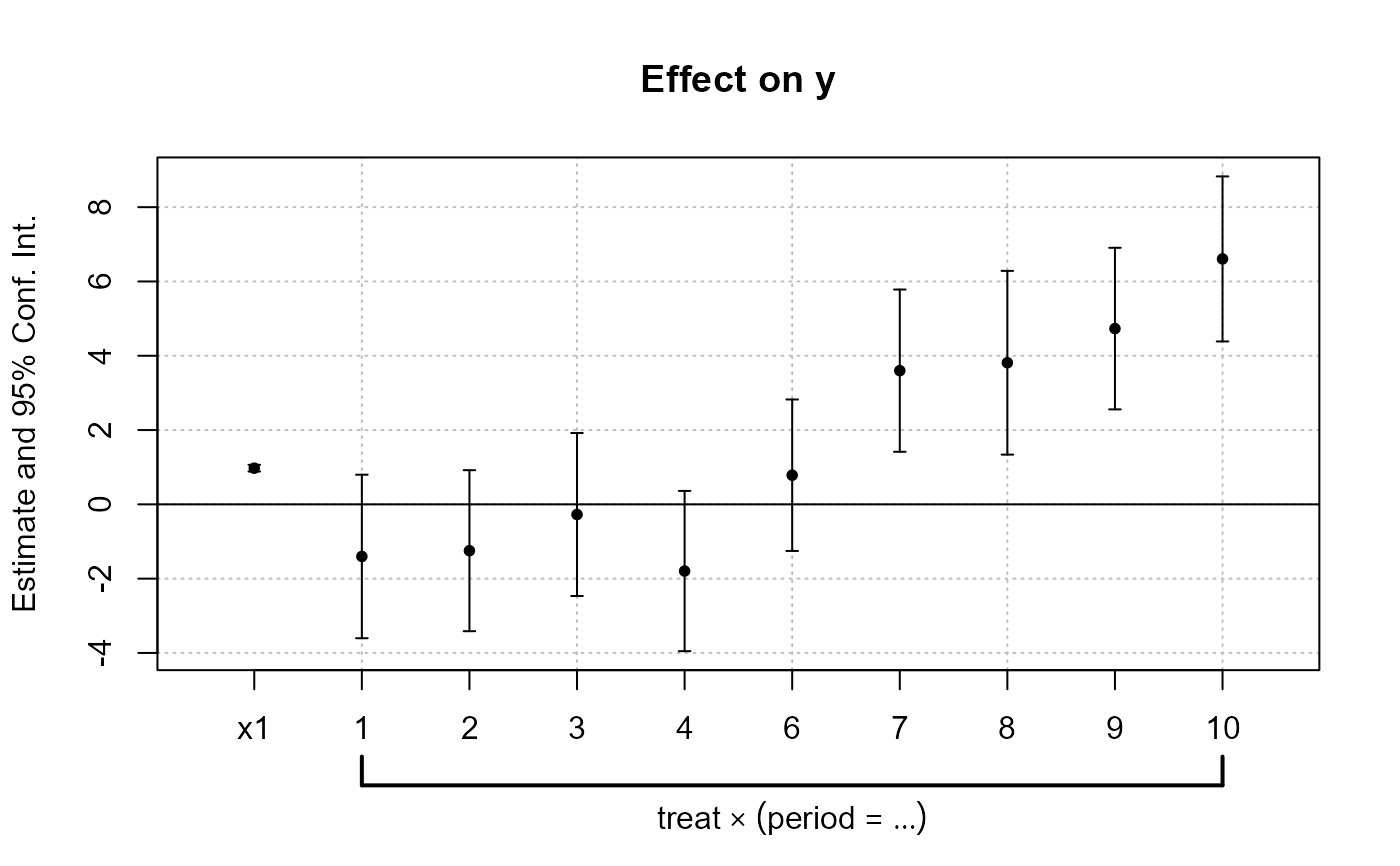
iplot(est_did, ref.line = FALSE, pt.join = TRUE)
# We can see that the graph is different from before:
# - only interactions are shown,
# - the reference is present,
# => this is fully flexible
iplot(est_did, ref.line = FALSE, pt.join = TRUE)
 #
# What if the interacted variable is not numeric?
# Let's create a "month" variable
all_months = c("aug", "sept", "oct", "nov", "dec", "jan",
"feb", "mar", "apr", "may", "jun", "jul")
base_inter$period_month = all_months[base_inter$period]
# The new estimation
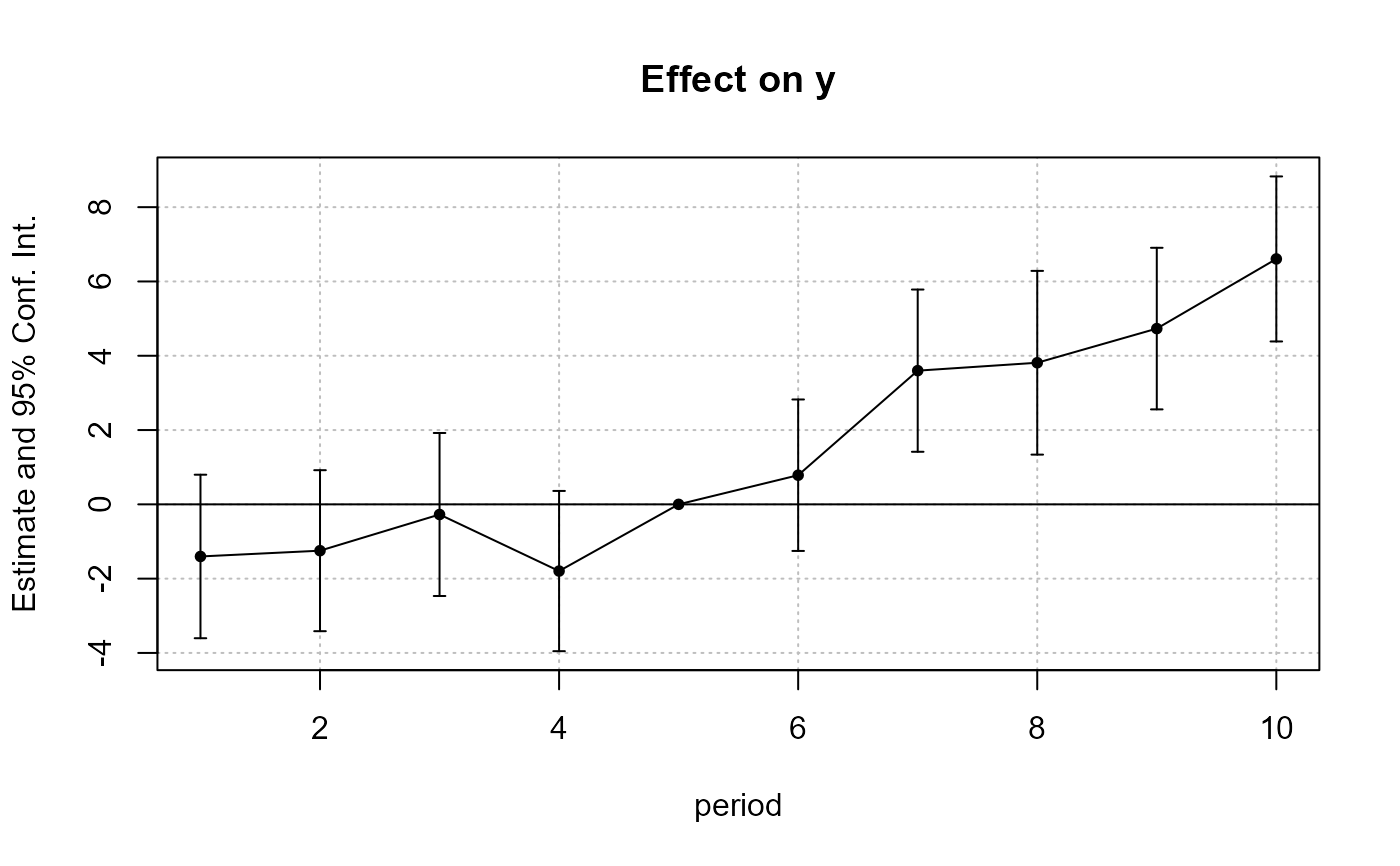
est = feols(y ~ x1 + i(period_month, treat, "oct") | id+period, base_inter)
# Since 'period_month' of type character, coefplot sorts it
iplot(est)
#
# What if the interacted variable is not numeric?
# Let's create a "month" variable
all_months = c("aug", "sept", "oct", "nov", "dec", "jan",
"feb", "mar", "apr", "may", "jun", "jul")
base_inter$period_month = all_months[base_inter$period]
# The new estimation
est = feols(y ~ x1 + i(period_month, treat, "oct") | id+period, base_inter)
# Since 'period_month' of type character, coefplot sorts it
iplot(est)
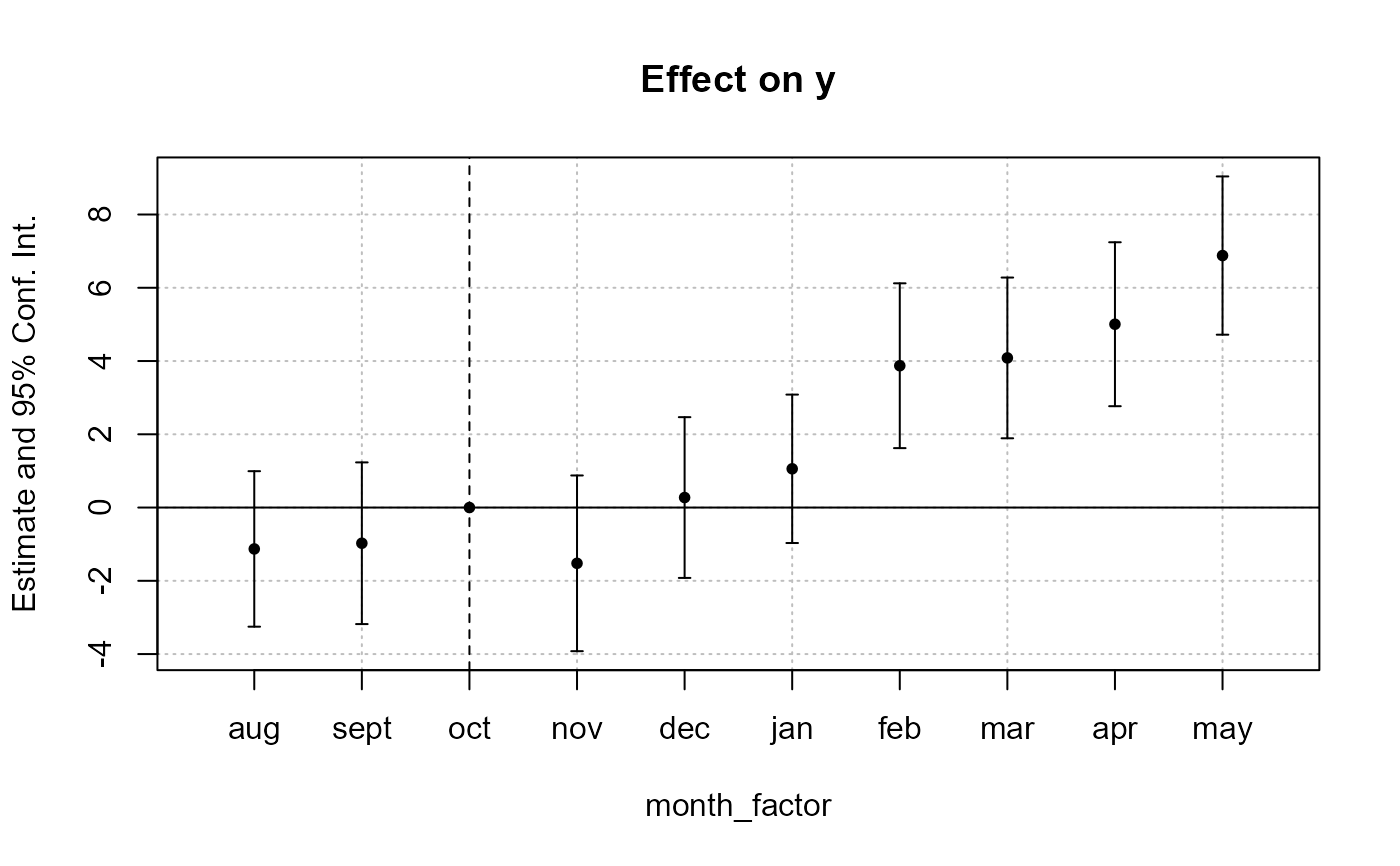
 # To respect a plotting order, use a factor
base_inter$month_factor = factor(base_inter$period_month, levels = all_months)
est = feols(y ~ x1 + i(month_factor, treat, "oct") | id + period, base_inter)
iplot(est)
# To respect a plotting order, use a factor
base_inter$month_factor = factor(base_inter$period_month, levels = all_months)
est = feols(y ~ x1 + i(month_factor, treat, "oct") | id + period, base_inter)
iplot(est)
 #
# Example 3: Setting defaults
#
# coefplot has many arguments, which makes it highly flexible.
# If you don't like the default style of coefplot. No worries,
# you can set *your* default by using the function
# setFixest_coefplot()
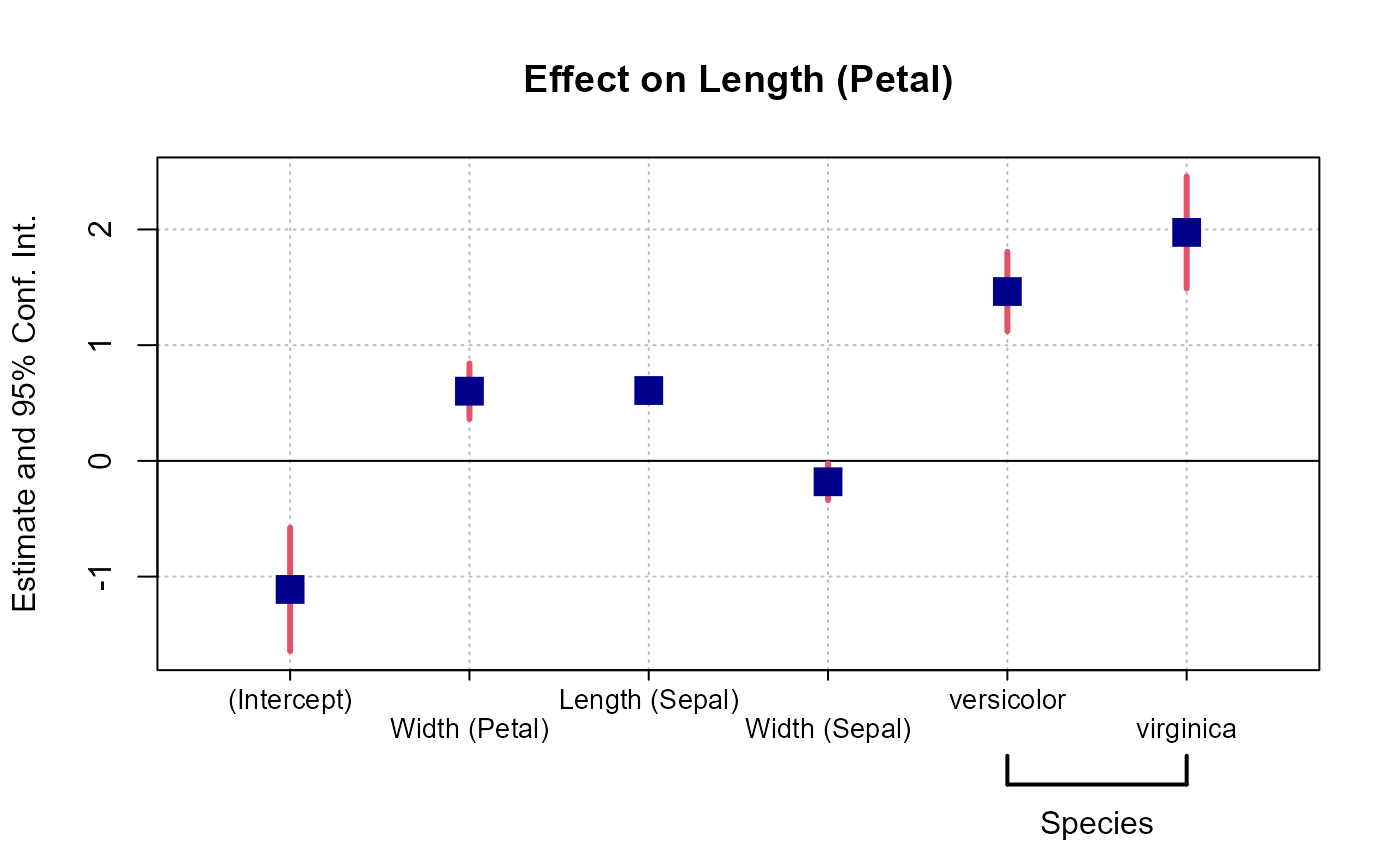
dict = c("Petal.Length"="Length (Petal)", "Petal.Width"="Width (Petal)",
"Sepal.Length"="Length (Sepal)", "Sepal.Width"="Width (Sepal)")
setFixest_coefplot(ci.col = 2, pt.col = "darkblue", ci.lwd = 3,
pt.cex = 2, pt.pch = 15, ci.width = 0, dict = dict)
est = feols(Petal.Length ~ Petal.Width + Sepal.Length +
Sepal.Width + i(Species), iris)
# And that's it
coefplot(est)
#
# Example 3: Setting defaults
#
# coefplot has many arguments, which makes it highly flexible.
# If you don't like the default style of coefplot. No worries,
# you can set *your* default by using the function
# setFixest_coefplot()
dict = c("Petal.Length"="Length (Petal)", "Petal.Width"="Width (Petal)",
"Sepal.Length"="Length (Sepal)", "Sepal.Width"="Width (Sepal)")
setFixest_coefplot(ci.col = 2, pt.col = "darkblue", ci.lwd = 3,
pt.cex = 2, pt.pch = 15, ci.width = 0, dict = dict)
est = feols(Petal.Length ~ Petal.Width + Sepal.Length +
Sepal.Width + i(Species), iris)
# And that's it
coefplot(est)
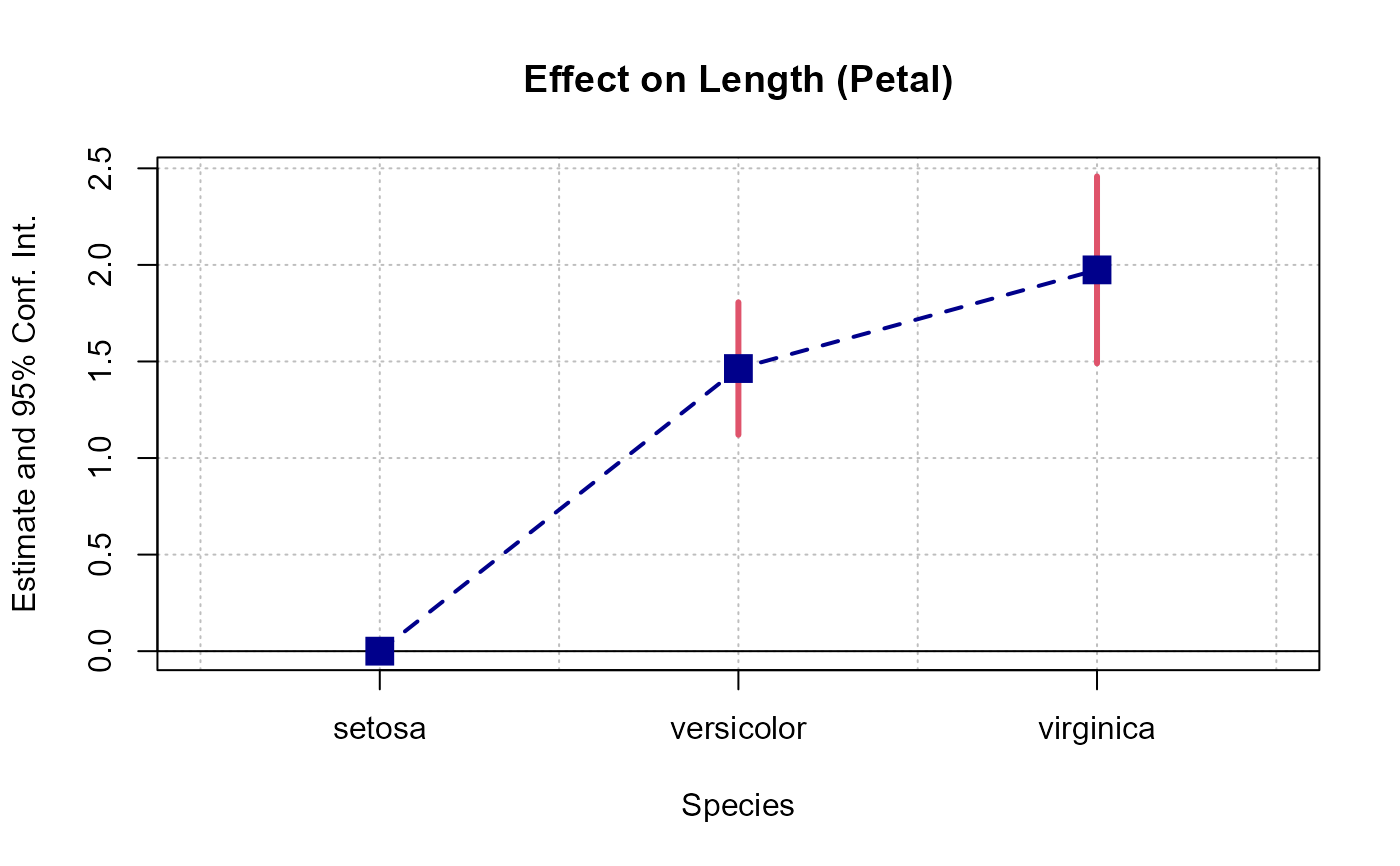
 # You can set separate default values for iplot
setFixest_coefplot("iplot", pt.join = TRUE, pt.join.par = list(lwd = 2, lty = 2))
iplot(est)
# You can set separate default values for iplot
setFixest_coefplot("iplot", pt.join = TRUE, pt.join.par = list(lwd = 2, lty = 2))
iplot(est)
 # To reset to the default settings:
setFixest_coefplot("all", reset = TRUE)
coefplot(est)
# To reset to the default settings:
setFixest_coefplot("all", reset = TRUE)
coefplot(est)
 #
# Example 4: group + cleaning
#
# You can use the argument group to group variables
# You can further use the special character "^^" to clean
# the beginning of the coef. name: particularly useful for factors
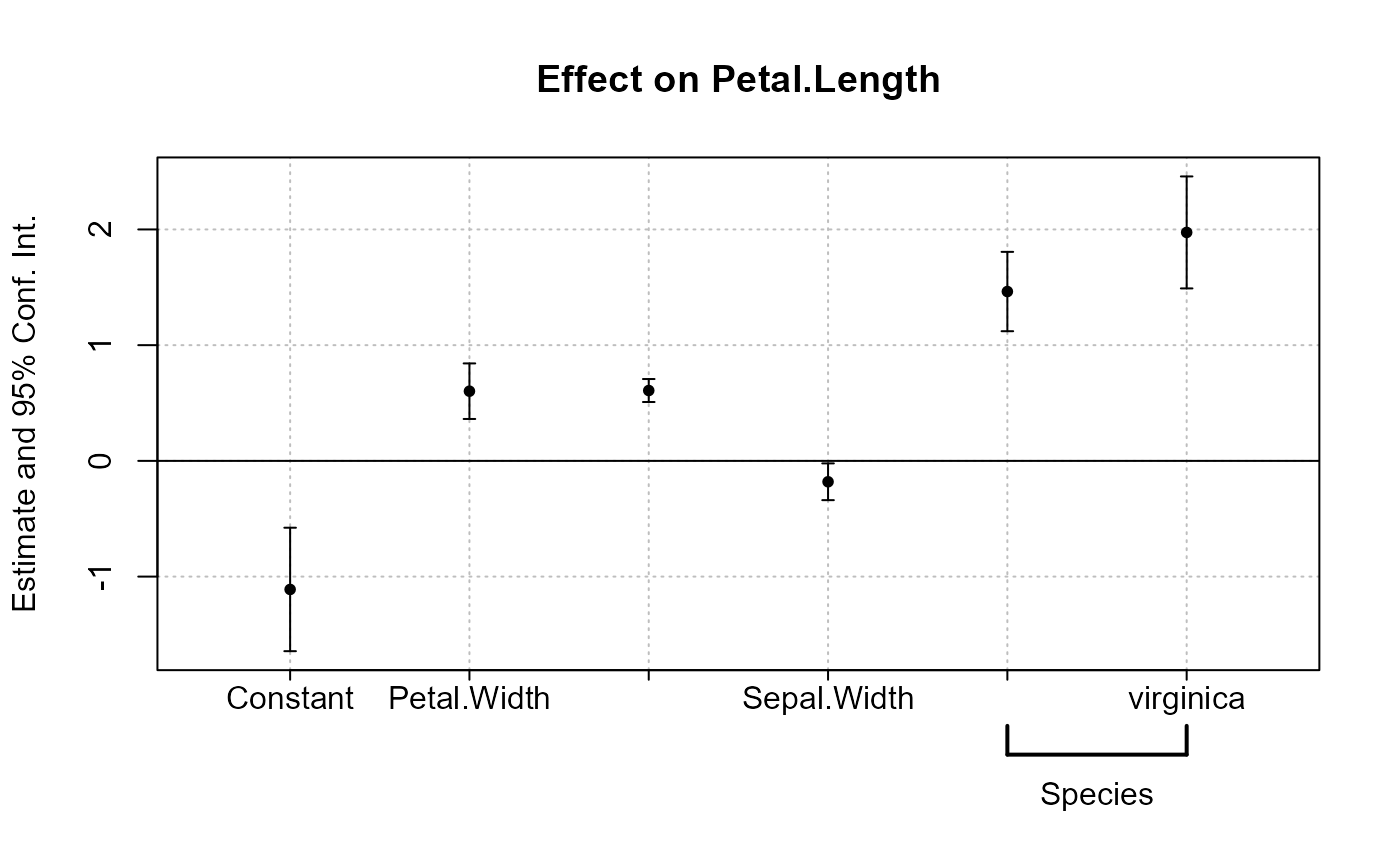
est = feols(Petal.Length ~ Petal.Width + Sepal.Length +
Sepal.Width + Species, iris)
# No grouping:
coefplot(est)
# now we group by Sepal and Species
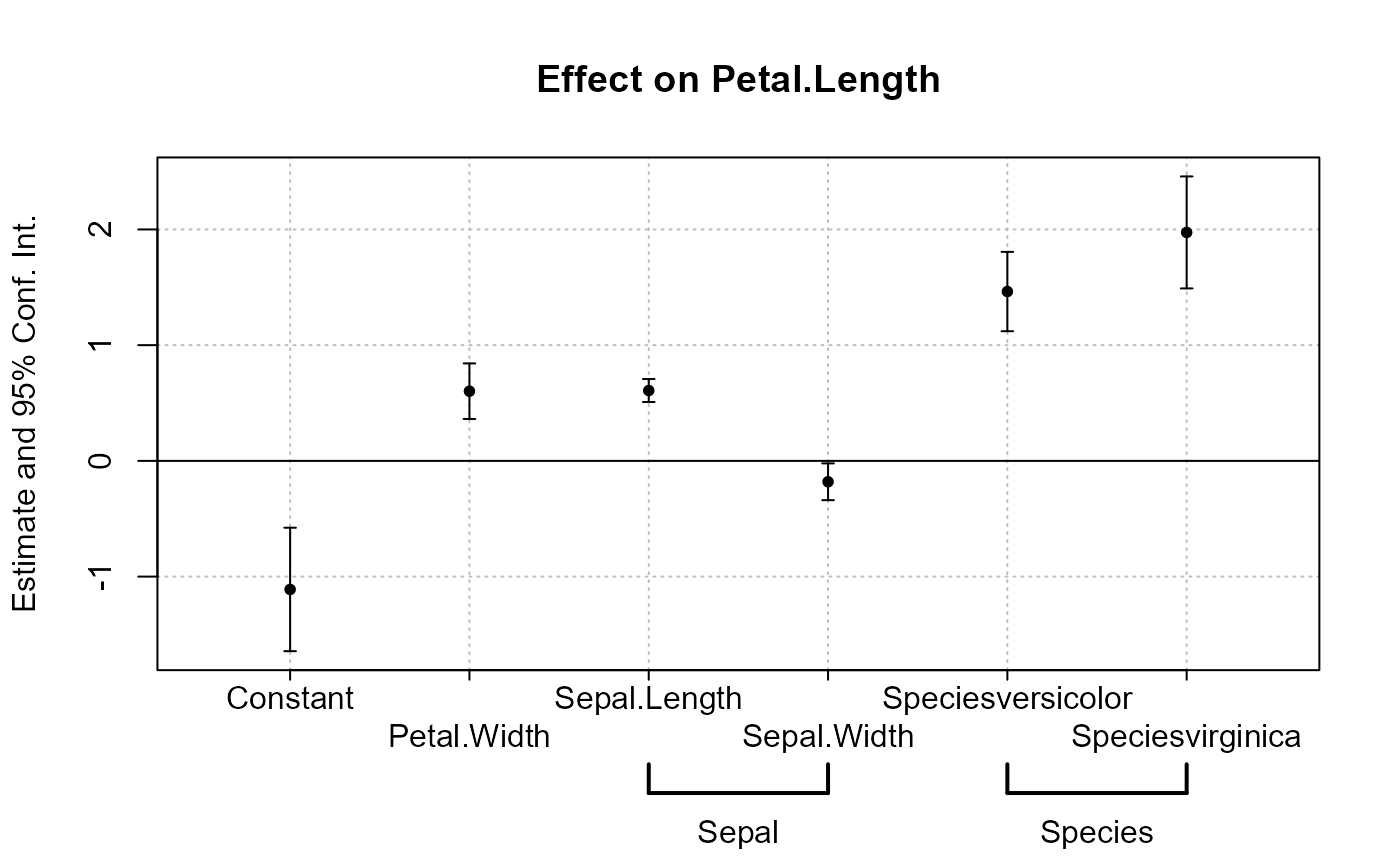
coefplot(est, group = list(Sepal = "Sepal", Species = "Species"))
#
# Example 4: group + cleaning
#
# You can use the argument group to group variables
# You can further use the special character "^^" to clean
# the beginning of the coef. name: particularly useful for factors
est = feols(Petal.Length ~ Petal.Width + Sepal.Length +
Sepal.Width + Species, iris)
# No grouping:
coefplot(est)
# now we group by Sepal and Species
coefplot(est, group = list(Sepal = "Sepal", Species = "Species"))
 # now we group + clean the beginning of the names using the special character ^^
coefplot(est, group = list(Sepal = "^^Sepal.", Species = "^^Species"))
# now we group + clean the beginning of the names using the special character ^^
coefplot(est, group = list(Sepal = "^^Sepal.", Species = "^^Species"))