fplot walkthrough

fplot plots of distributions, automatically adjusting the parameters for the user. The syntax uses formulas, allowing conditional/weighted distributions with minimum efforts. The many arguments are automatically adjusted to provide the most meaningful (and hopefully beautiful!) graphs depending on the data at hand.

Although the core of the package concerns distributions, fplot also offers functions to plot trends (possibly conditional) and conditional boxplots.

Since the main purpose of this package is to provide graphs ready for publications, you can globally relabel all the variables to be displayed with setFplot_dict. In this vignette this is done once:

setFplot_dict(c(Origin = "Exporting Country", Destination = "Importing Country", Euros = "Exports Value in €", jnl_top_25p = "Pub. in Top 25% journal", jnl_top_5p = "Publications in Top 5% journal", journal = "Journal", institution = "U.S. Institution", Petal.Length = "Petal Length"))

Distributions

The function plot_distr plots distributions. The syntax of the function plot_distr is as follows:

plot_distr(weight(s) ~ variable | moderator, data)

This function is extremely versatile: its default behavior totally depends on the data it deals with.

Categorical data

We will use data on publications extracted from the Microsoft Academic Graph.

library(fplot)
data(us_pub_econ, package = "fplot")

This data corresponds to publications from U.S. institution in the field of economics in the period 1985-1990. Here is a sample of the data:

paper_id	year	institution	journal	jnl_top_25p
865948	1988	university of california berkeley	university of san francisco law review	0
2027349	1990	university of wisconsin madison	climatic change	1
2299436	1988	columbia university	marine resource economics	0
2558483	1988	yale university	journal of accounting auditing & finance	0
2672463	1989	university of michigan	administration in social work	0
2860349	1985	university of kansas	administration in social work	0

What’s the distribution of publications per institutions?

# When there is only one variable, you can use a vector
plot_distr(us_pub_econ$institution)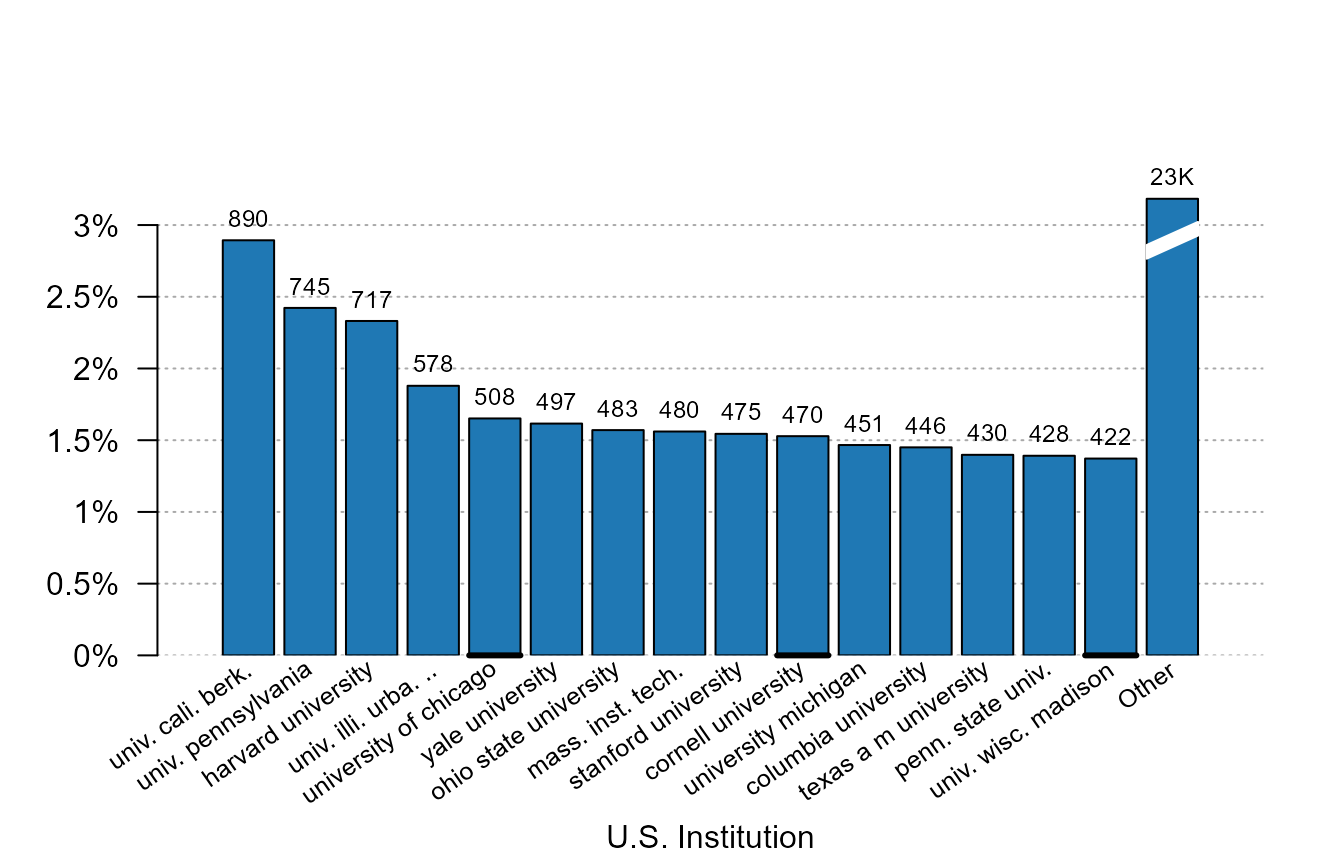

What can we remark? First only the first 15 most important institutions are plotted. Indeed, since the institution variable is a categorical data, plotting all the 444 different would have just cluttered the graph and nothing could have been visible. We can increase the number of bars plotted with argument nbins.

Although only the first are plotted, we still have information on the institutions left with the last (broken) bar reporting the number of publications that are left. We can avoid displaying this column with the argument other = FALSE.

We can also notice that not only the graph of the distribution is shown, but the number of observations is reported on the top of each bar to have a quick insight of the total numbers. Further, the size of the numbers always fit the width of the bars. The argument top manages the information displayed on the top of the bars: it can be numbers (top = "nb"), fractions (top = "frac"), or nothing (top = "none"). The default depends on the type of data.

Finally, the labels in the x-axis: i) all appear and ii) are truncated meaningfully. Since the institution variable is categorical, there is no way to deduce which institution each bar represent if it is not displayed explicitly. They are further truncated at 20 characters (argument trunc) and the truncation method tries to keep the most information from the labels (trunc.method = "auto"). But there are other truncation methods, like trimming the right (resp. the middle) of the label with trunc.method = "right" (resp. trunc.method = "mid"). To display horizontal labels instead, you can use labels.tilted = FALSE.

Now let’s weight the production of the institutions by the quality of the journals:

plot_distr(jnl_top_5p ~ institution, us_pub_econ)

We added the weight directly in the left-hand-side of the formula. Notice that now Harvard ranks 1st (it was 3rd when not weighting by quality).

We can add several weights at the same time:

plot_distr(1 + jnl_top_25p + jnl_top_5p ~ institution, us_pub_econ)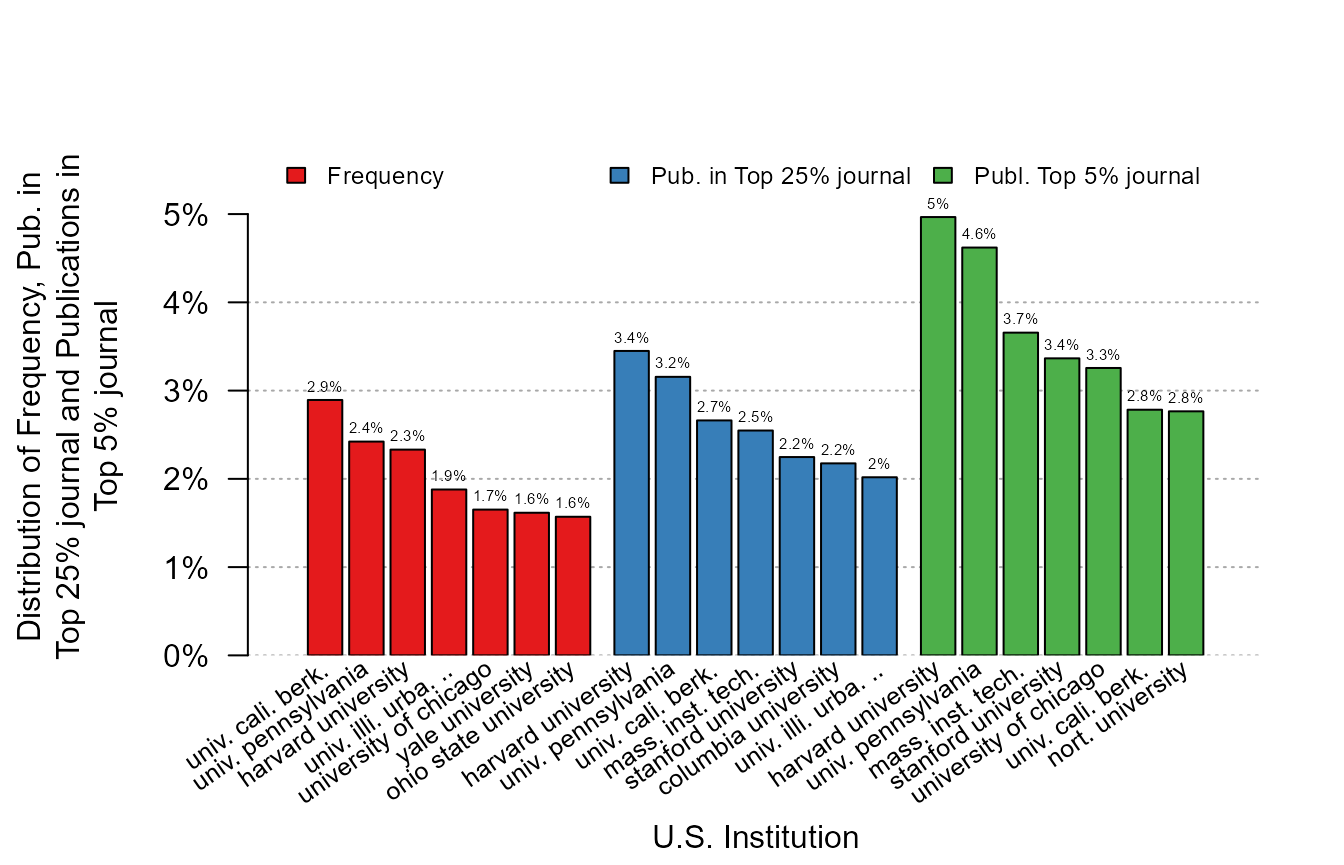

As we can see, the more we weight by quality, the more the distribution is skewed towards the top institutions.

Now we illustrate the conditional graphs by asking the question of what are the journals in which the 3 most productive institutions publish.

plot_distr(~ journal | institution, us_pub_econ)
#> The 3 moderators were chosen based on frequency.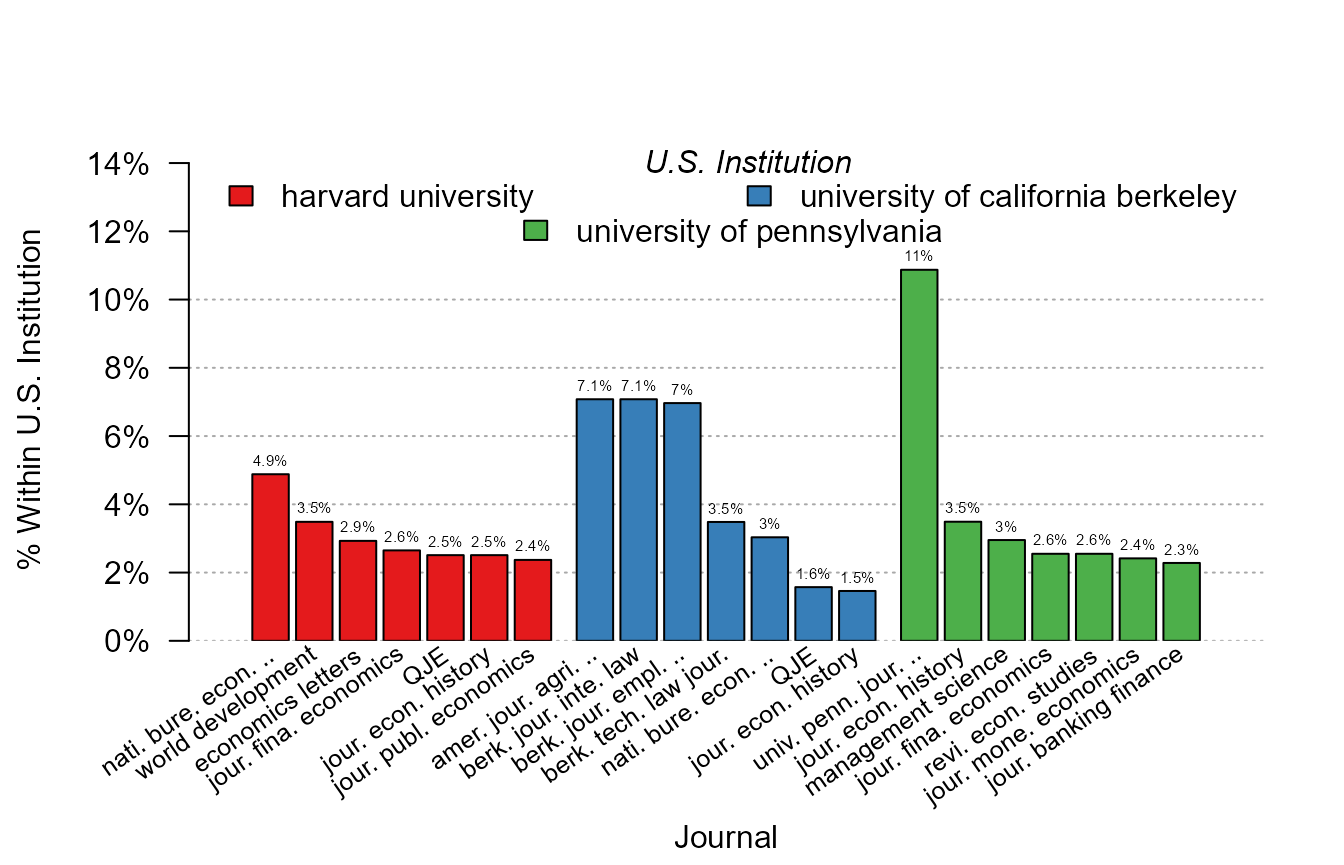

What happened? In the x-axis, the journals are displayed since they are the “variable”, and since we added the institution as a moderator, the data is broken down across each institution. But not all the 444 institutions are shown: by default only the three moderator values (here institutions) that appear the most are reported. When there is an automatic selection, a message is also prompted. The user can increase the number of moderator values reported with the argument mod.select, or provide the specific values to be shown.

The 7 most important journals are displayed for each institution and the scale corresponds to the share of the journal within the institution. Instead of displaying the within share, the total share could have been displayed with the option total = TRUE.

Here the numbers on the top of the bars come handy to provide comparisons across institutions. Importantly, because the journal names are long, it would have been impossible to display them in a standard way. As we can see, they are first truncated (meaningfully) and then tilted. in the end, the graph is fully informative.

By default, when the data is split, the bar containing the “other” information is not displayed to save space. But of course, we can add it with the appropriate option:

# Previous graph + "other" column
plot_distr(~ journal | institution, us_pub_econ, other = TRUE)
#> The 3 moderators were chosen based on frequency.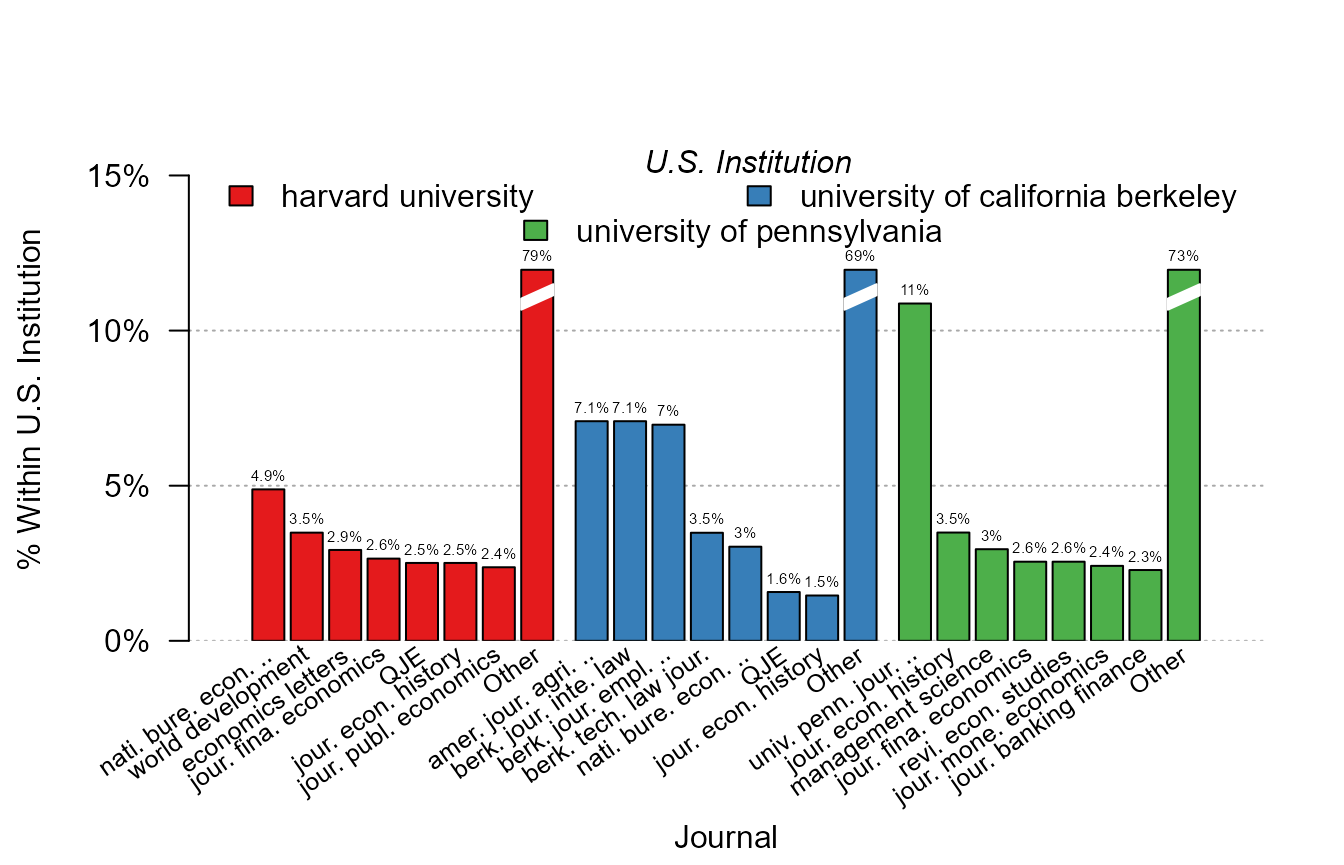

If you wish to select other moderator values, you can use mod.select with regular expressions. Let’s have a look at three Massachusetts institutions:

plot_distr(~ journal | institution, us_pub_econ, mod.select = "harvard|boston.+uni|mass.+inst")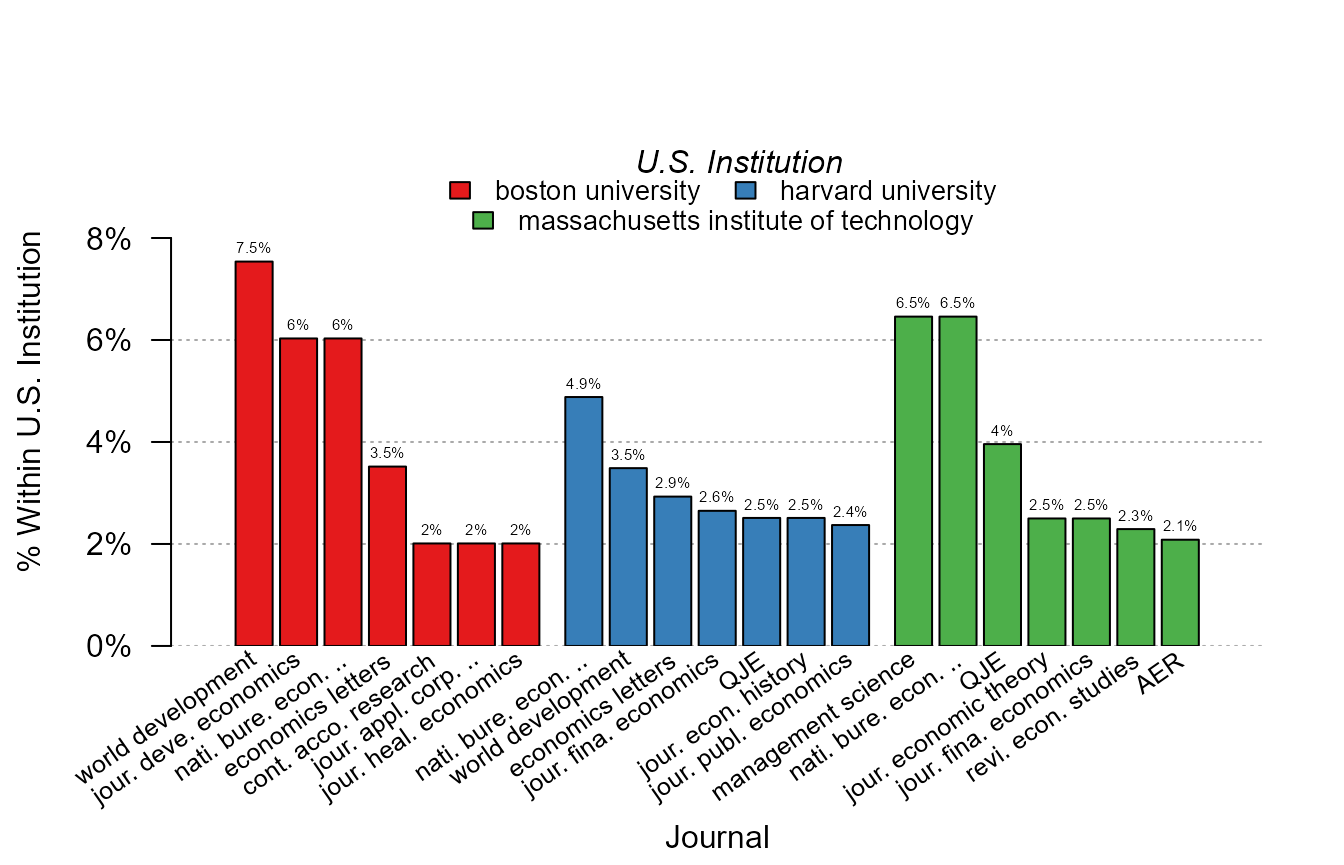

Numeric data

Now let’s illustrate the behavior of the function in presence of numerical data. We first import trade data:

data(trade, package = "fixest")
head(trade)

Destination	Origin	Product	Year	dist_km	Euros
LU	BE	1	2007	139.5719	2966697
BE	LU	1	2007	139.5719	6755030
LU	BE	2	2007	139.5719	57078782
BE	LU	2	2007	139.5719	7117406
LU	BE	3	2007	139.5719	17379821
BE	LU	3	2007	139.5719	2622254

This data consists of importations between pairs of European countries for different products across time. Let’s look at the distribution of trade volume:

plot_distr(trade$Euros)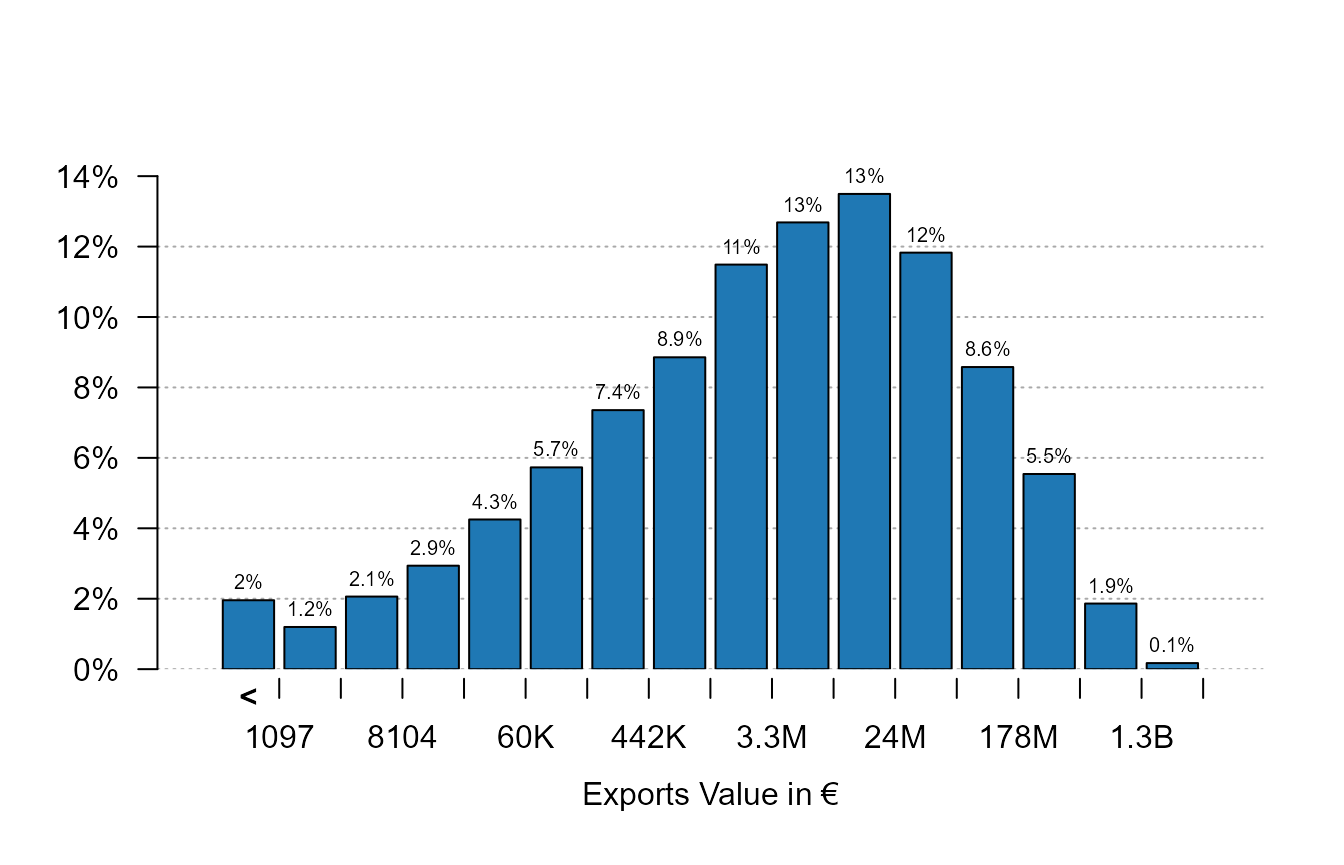

Three main things can be remarked. First, the data has been automatically set to logarithmic form beforehand in order to offer a better display. This behavior can be changed with the argument log. Second, the first column contains all the leftovers that are lower than 1,097 – this allows to focus on the part of the graph where there is the most variation. This is why the graph does not start from 0 but rather is focused on the mode of the distribution. Thanks to this first column, there is no loss of information while ensuring greater readability. Finally, the numeric scale is formatted for an easy reading.

Now let’s look at the distribution of French and German exports:

plot_distr(~ Euros | Origin, trade, mod.select = c("DE", "FR"))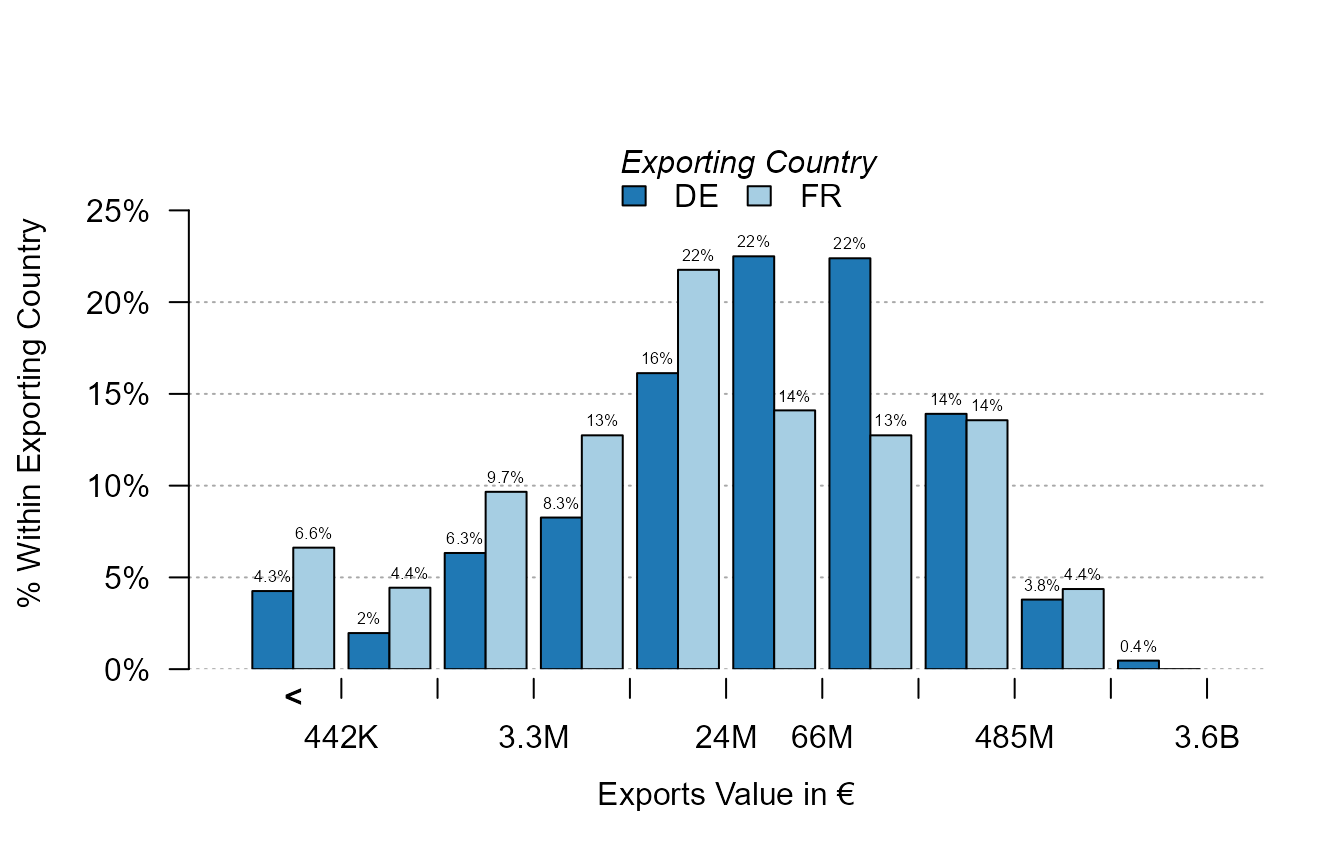

We use the argument mod.select to select the two moderator values. For each logarithmic “bin”, the two moderators are compared.

Now let’s look at another set of numeric data using the iris data set.

plot_distr(iris$Petal.Length)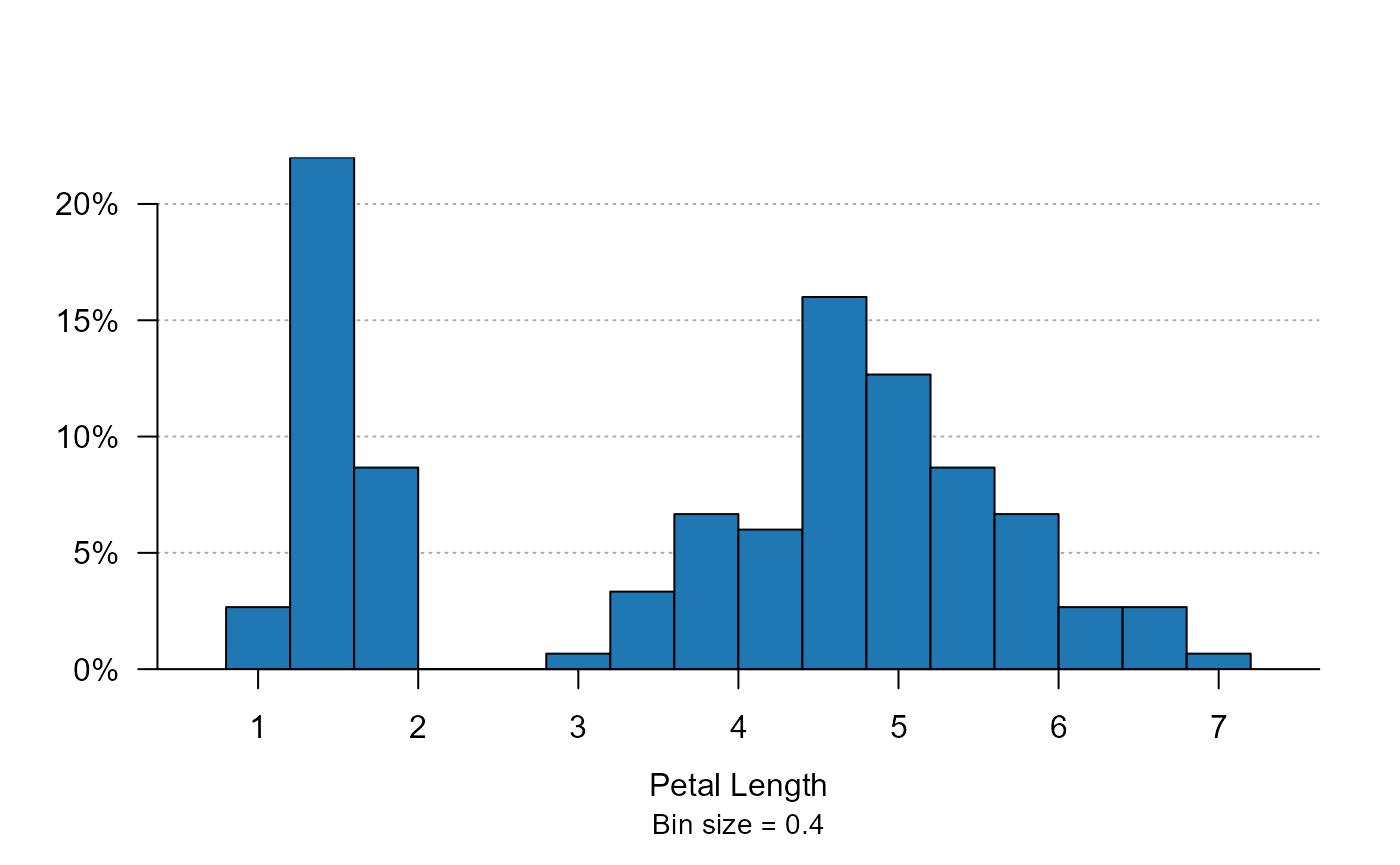

For “well distributed” continuous data, it looks very much like a regular histogram, but a bit nicer. Note that the bin size is always “discrete” to allow easy reading. Now we can also split the data by species:

plot_distr(~ Petal.Length | Species, iris)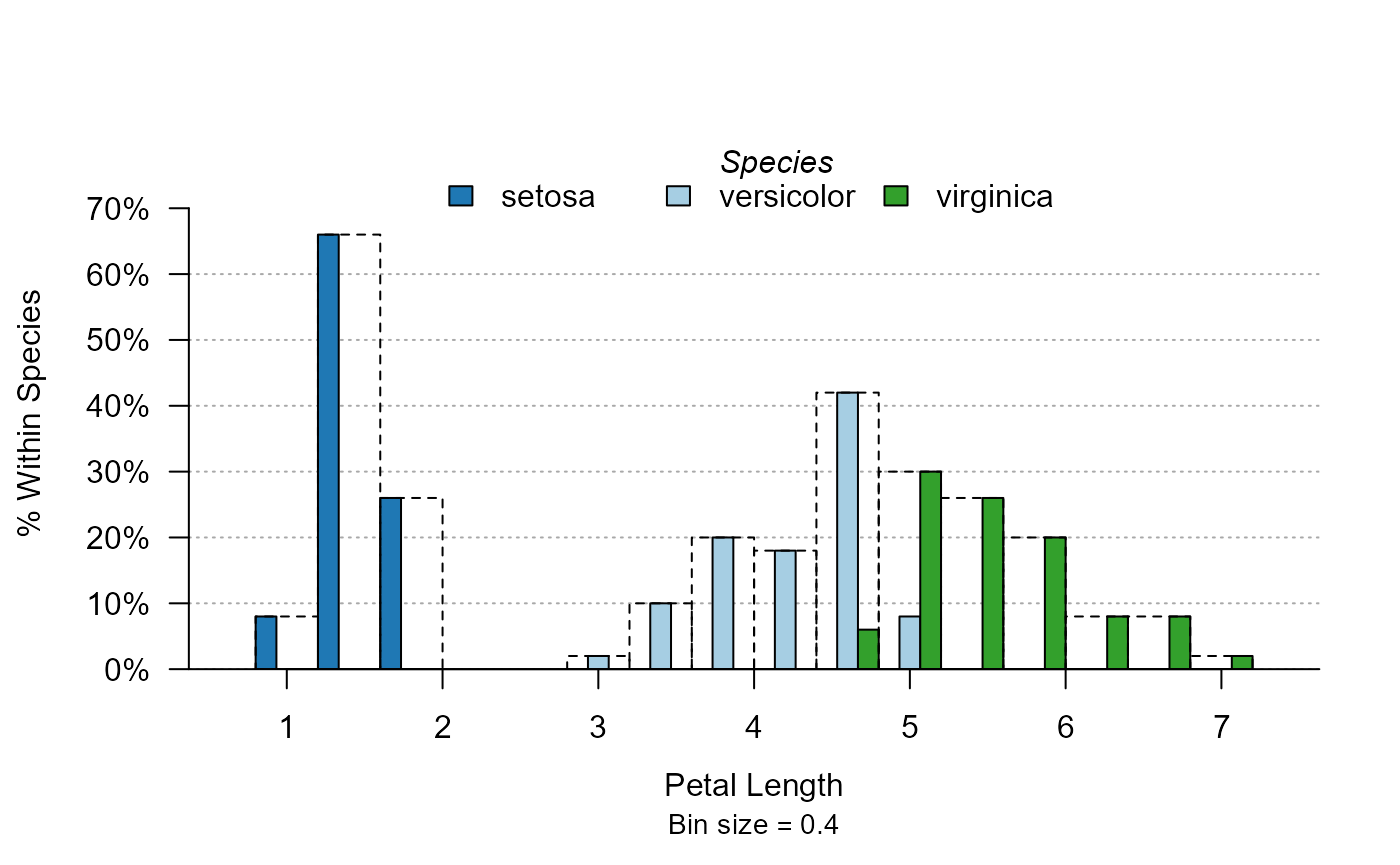

Note that the full widths of the bins are reported in dashed lines, so that the user does not confuse the size of the total bin with the size of the bin for one single species.

Instead of displaying the three species on the same axis, we could also choose to split the data:

plot_distr(~ Petal.Length | Species, iris, mod.method = "split")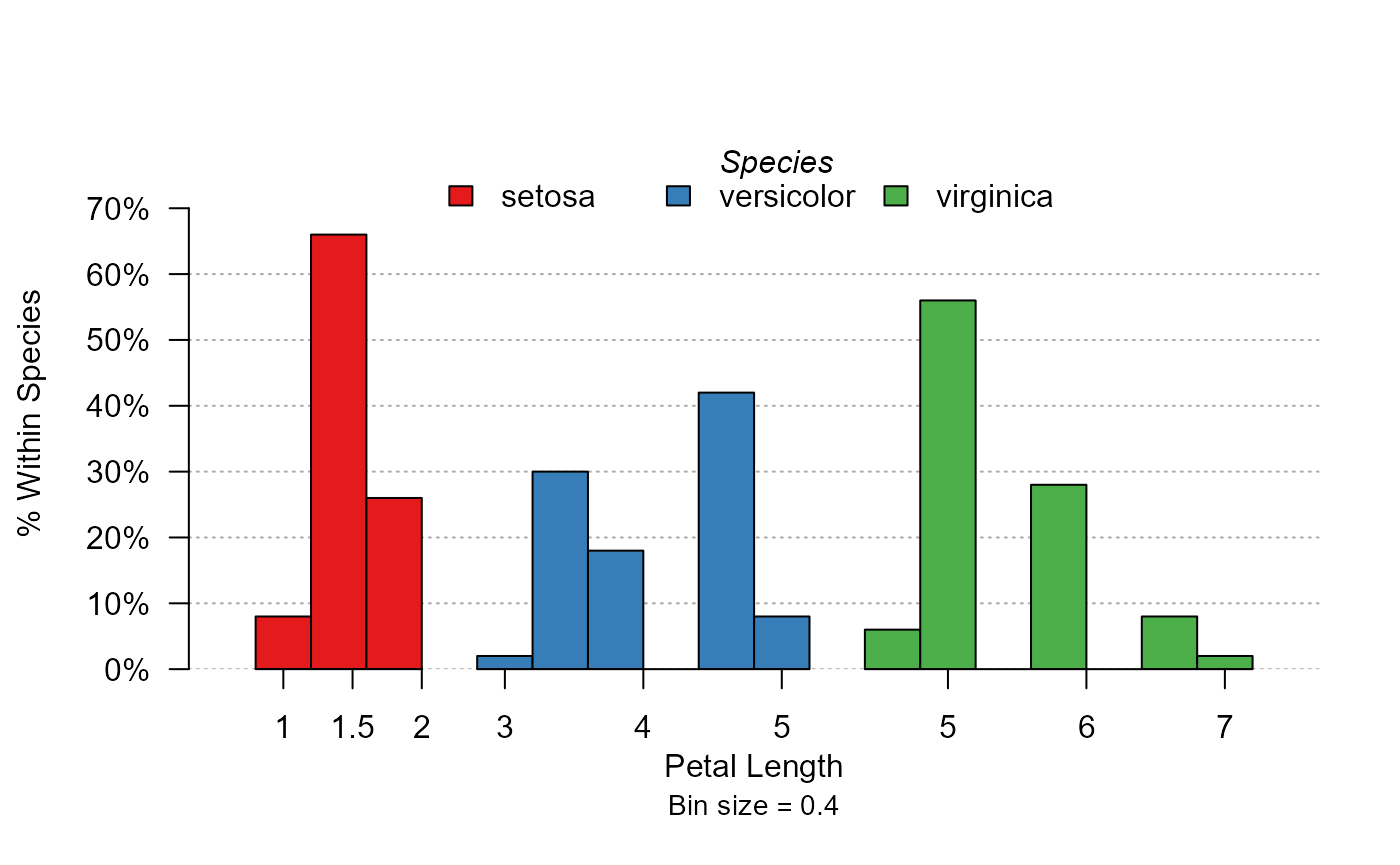

The full distribution of the three species are now separated.

Stacking

Another way to display moderators is by stacking their values. Let’s see the sepal length distribution by iris species:

plot_distr(~ Sepal.Length | Species, iris, mod.method = "stack")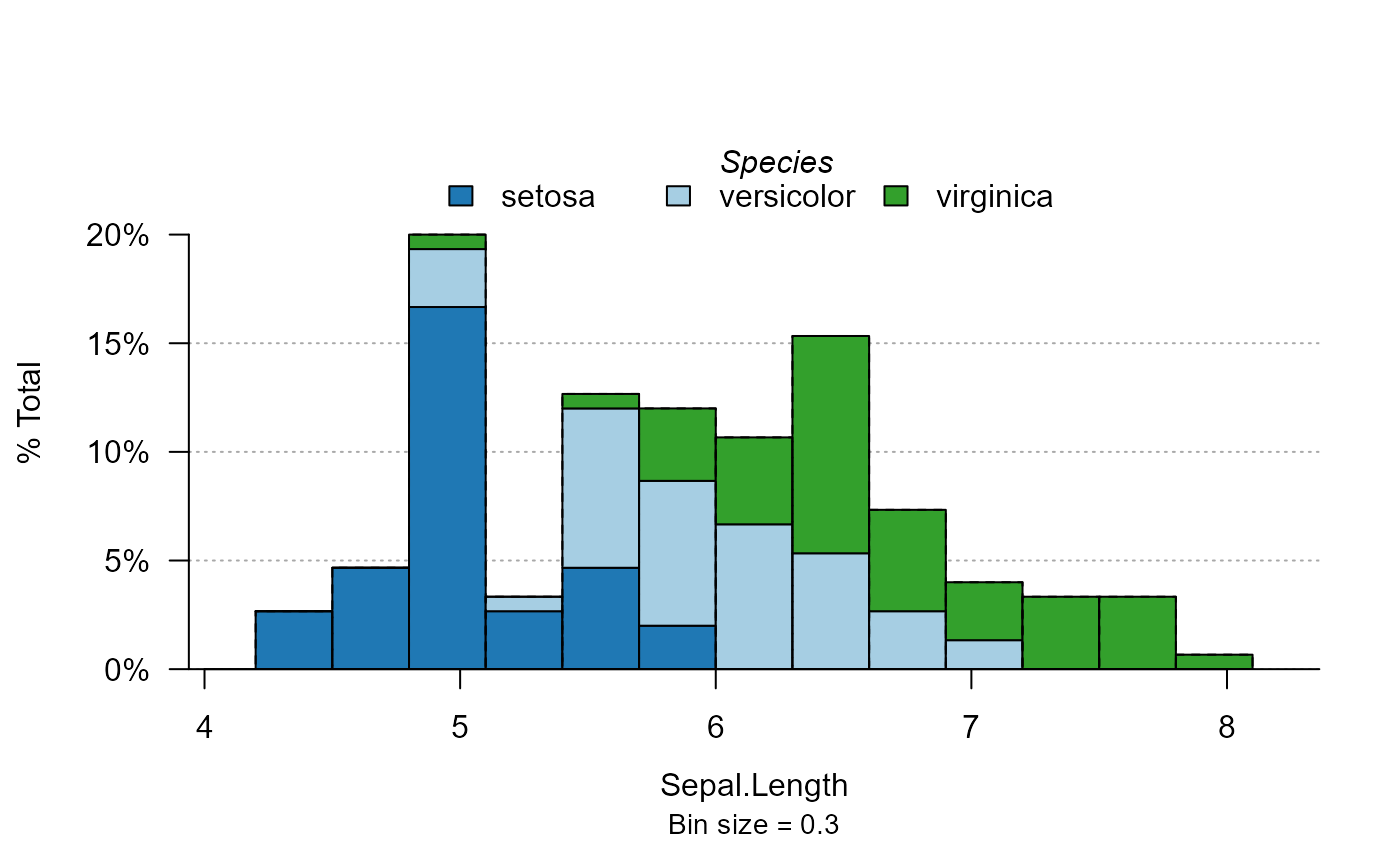

Cumulative distribution

To display the cumulative distribution, simply use the argument cumul = TRUE. Let’s look at the cumulative distribution of the top 5% publications:

plot_distr(jnl_top_5p ~ institution, us_pub_econ, cumul = TRUE)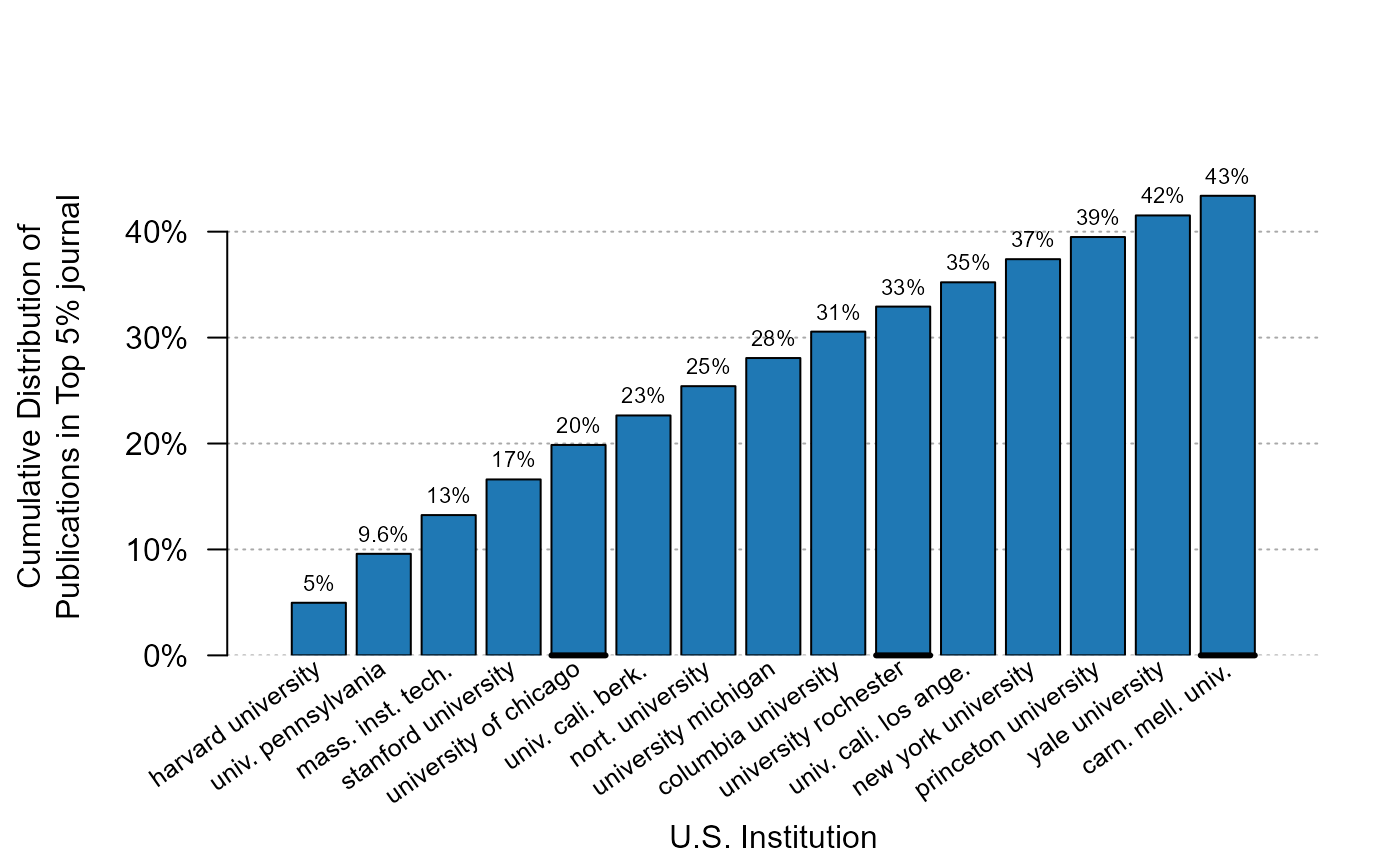

Just 10 institutions (the thick black line appears every five values) account for 33% of all top 5% publications.

Trends

You can also show the evolution of the aggregate of some variable using the function plot_lines. By default, the function applied by plot_lines is the average, but can be modified at will. Let’s look at the evolution of the fraction of publications published in top 5% journals:

plot_lines(jnl_top_5p ~ year, us_pub_econ)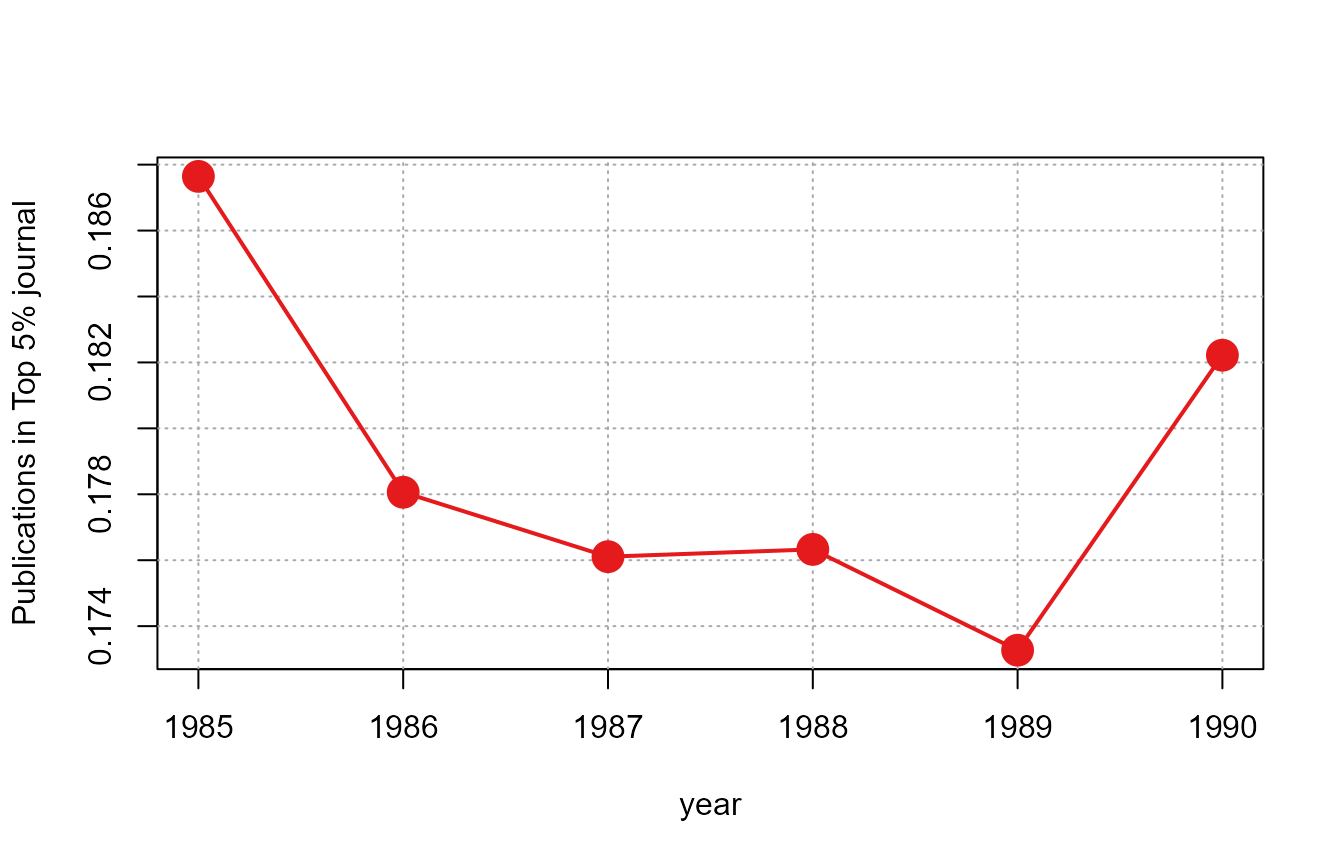

The data is first aggregated at the year level, i.e. mean(us_pub_econ[year == YEAR, jnl_top_5p]) is applied for each year, then a simple scatter plot is drawn.

As before, it is very easy to make the graph conditional. Let’s look at the evolution for the three top institutions:

# Let's find out the top 3/5 institutions in terms of production
# we use plot_distr without plotting:
info = plot_distr(us_pub_econ$institution, plot = FALSE)
top3_instit = head(info$x, 3)
top5_instit = head(info$x, 5)
plot_lines(jnl_top_5p ~ year | institution, 
           us_pub_econ[institution %in% top3_instit])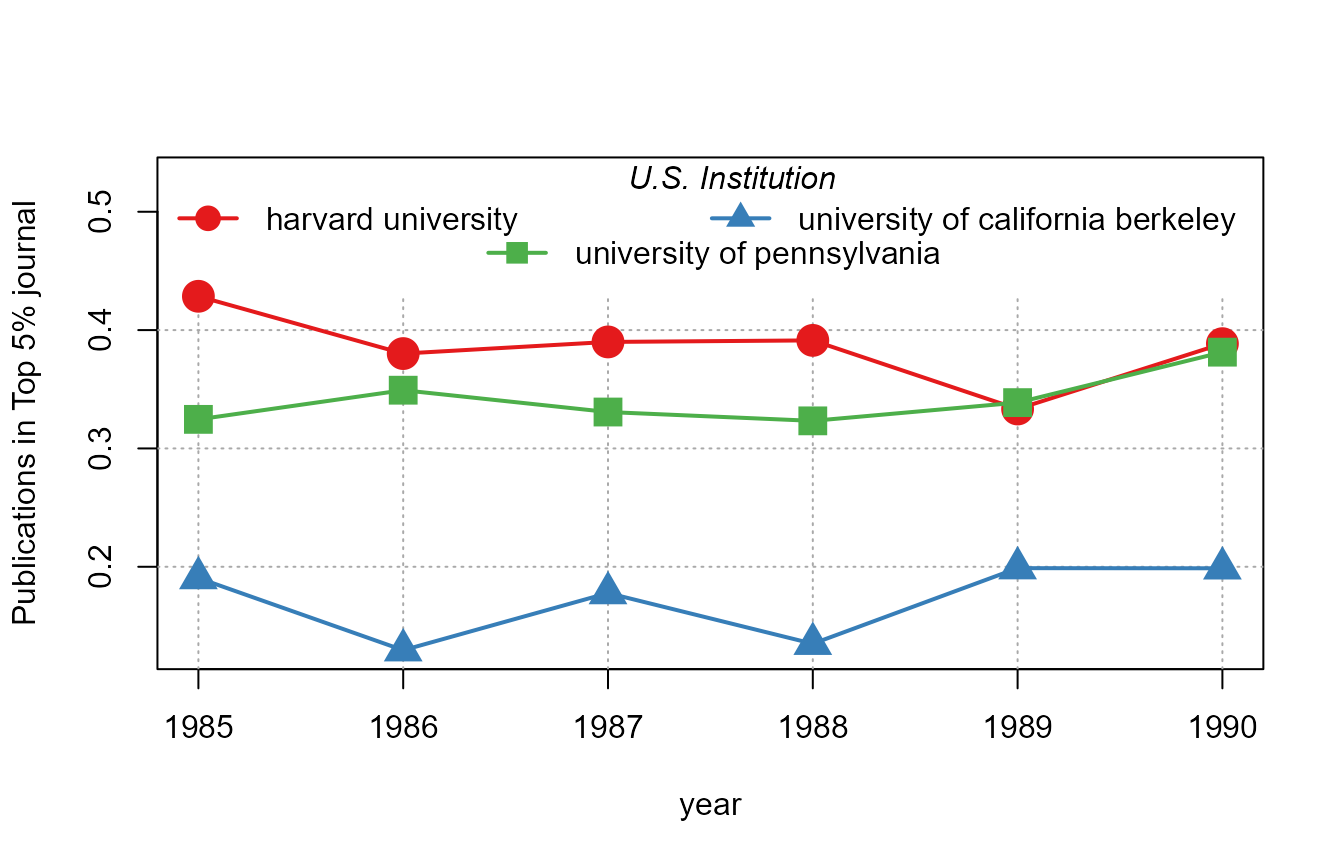

If we want to display the conditional evolution of the frequencies per year, we can use 1 as a variable, which will set the default function to sum in order to get the frequencies:

plot_lines(1 ~ year | institution, us_pub_econ[institution %in% top5_instit])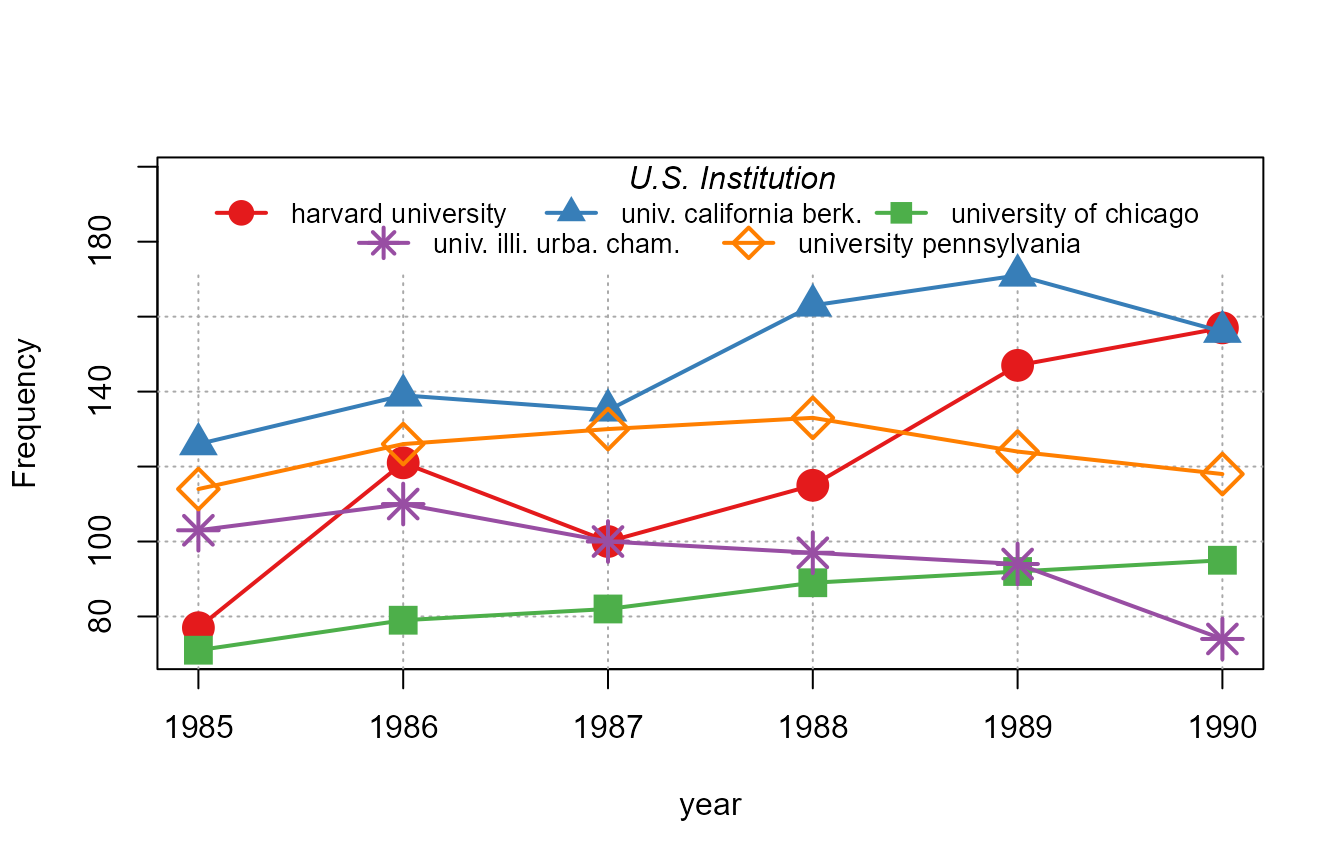

What can we remark from the previous graph? When the legend would not fit in one line, the algorithm automatically adds one line to display all the relevant information while using all the width of the graph for readability.

We can add some simple smoothing with the option smoothing_window:

plot_lines(1 ~ year | institution, us_pub_econ[institution %in% top5_instit], 
           smoothing_window = 1)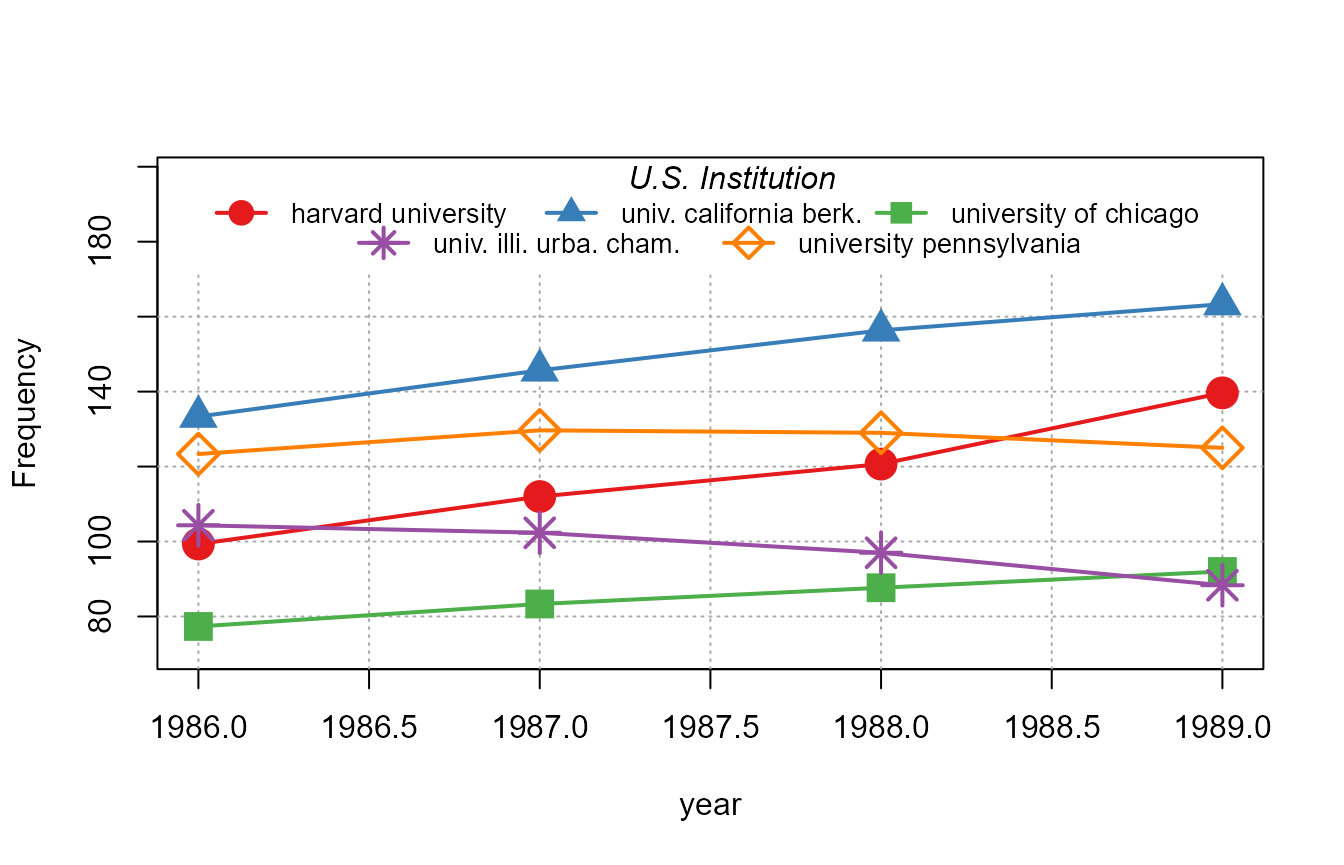

The smoothing uses the n\(^{th}\) future and past years to smooth the data.

Conditional boxplot

The function plot_box is made for conditional boxplots: one variable conditionally to one or two moderators. Let’s have an example with the publications data. First we create the number of publications in top 5% journals per year and per institution, then we display a yearly boxplot:

base_pub = us_pub_econ[, .(nb_pub_top_5 = sum(jnl_top_5p)), 
                          by = .(year, institution)]
plot_box(nb_pub_top_5 ~ year, base_pub)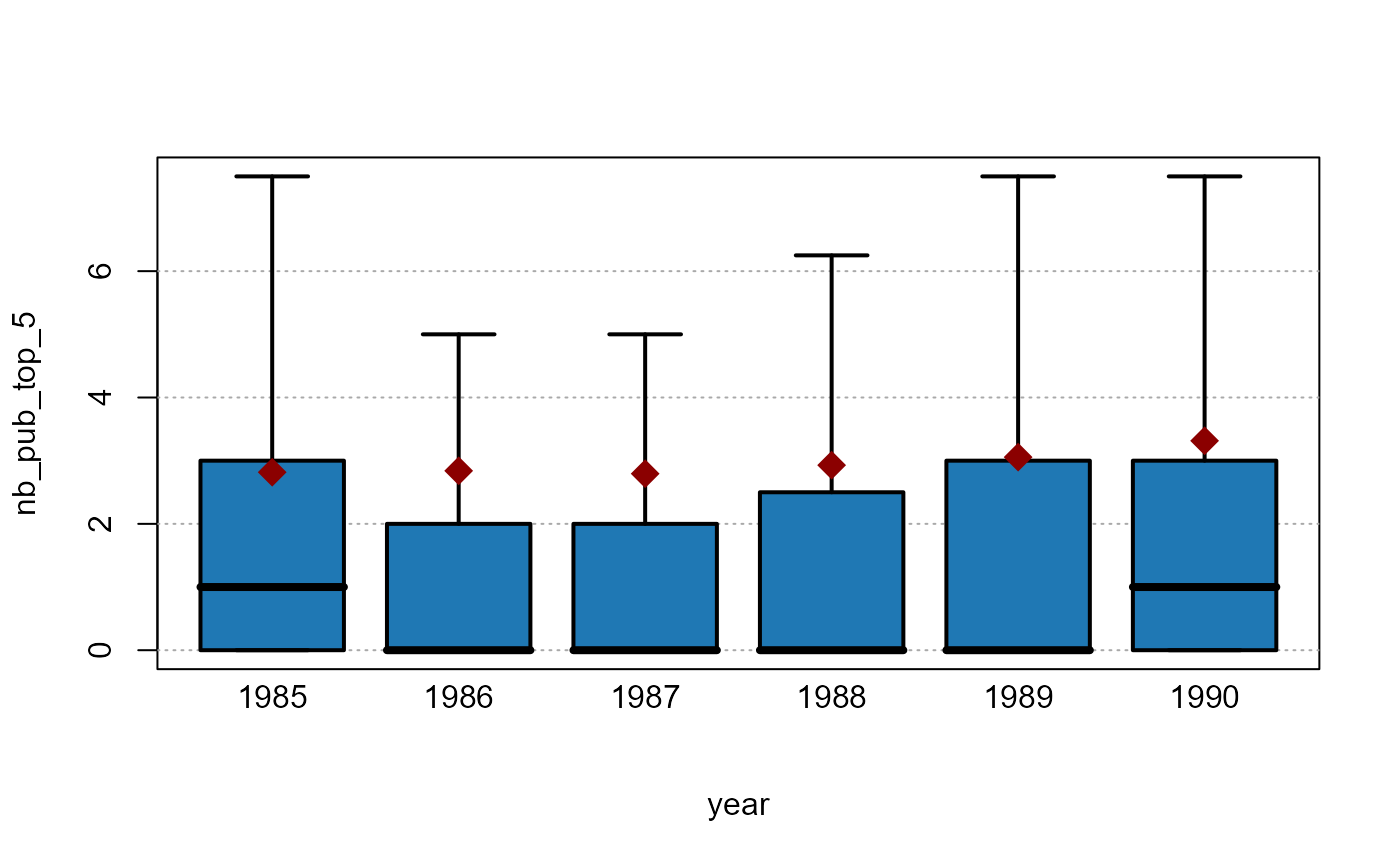

By default the outliers are not shown when the boxplots would disappear because of the scale of the outliers. The means however are displayed when the outliers are not, here it is represented by a red diamond. We can see that while the 3rd quartile almost doubled in the period, the mean almost trebled which means that the outliers gained weight over time.

Now let’s redo the same analysis but by distinguishing the top 5 institutions from the rest:

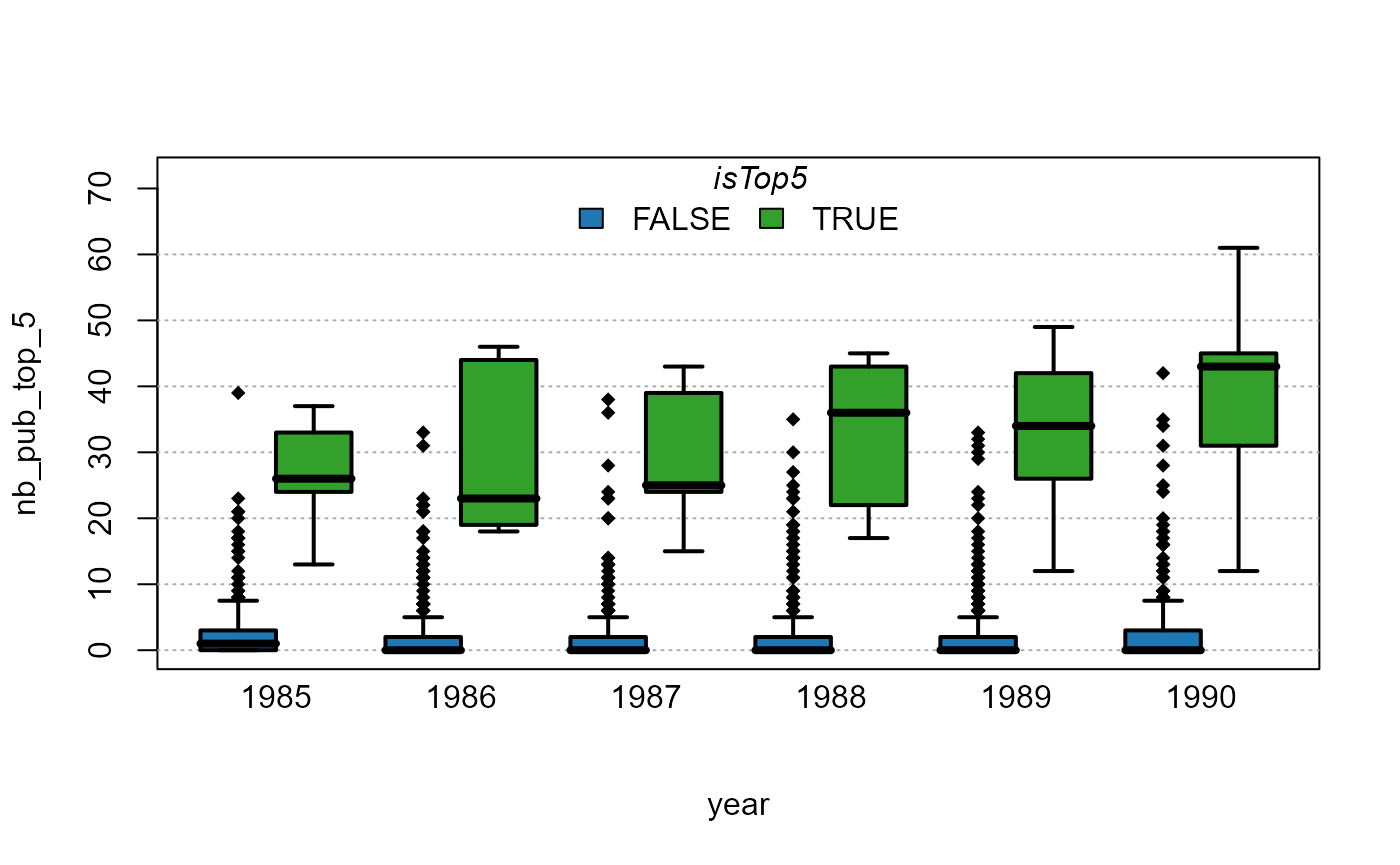
base_pub[, isTop5 := institution %in% top5_instit]
plot_box(nb_pub_top_5 ~ year | isTop5, base_pub)

Now the outliers are reported, to avoid this behavior, we can use the argument outlier = FALSE:

# we also drop the mean
plot_box(nb_pub_top_5 ~ year | isTop5, base_pub, outlier = FALSE)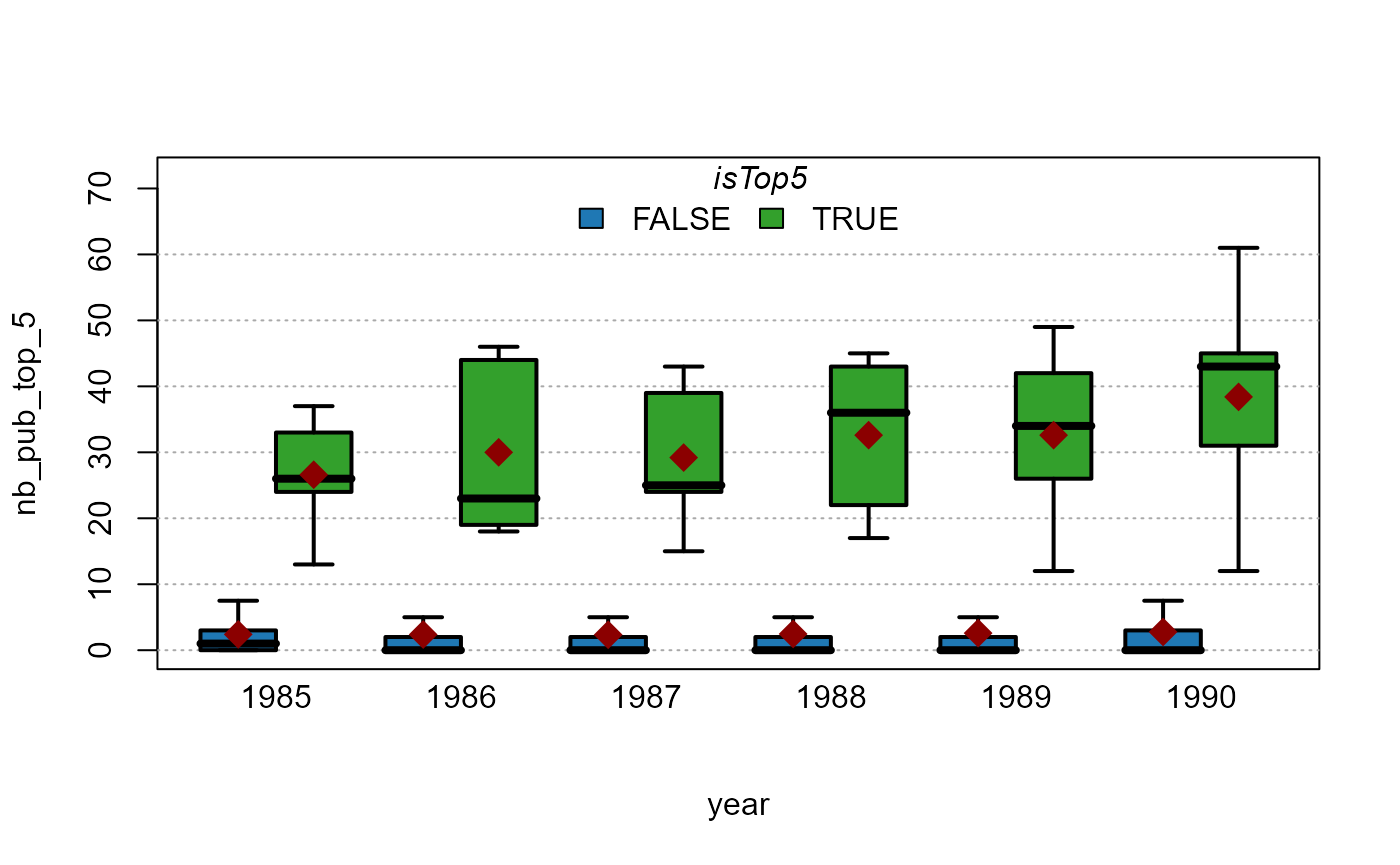

You can also plot several variables at once. Let’s take an example using iris data:

plot_box(. ~ Species, iris)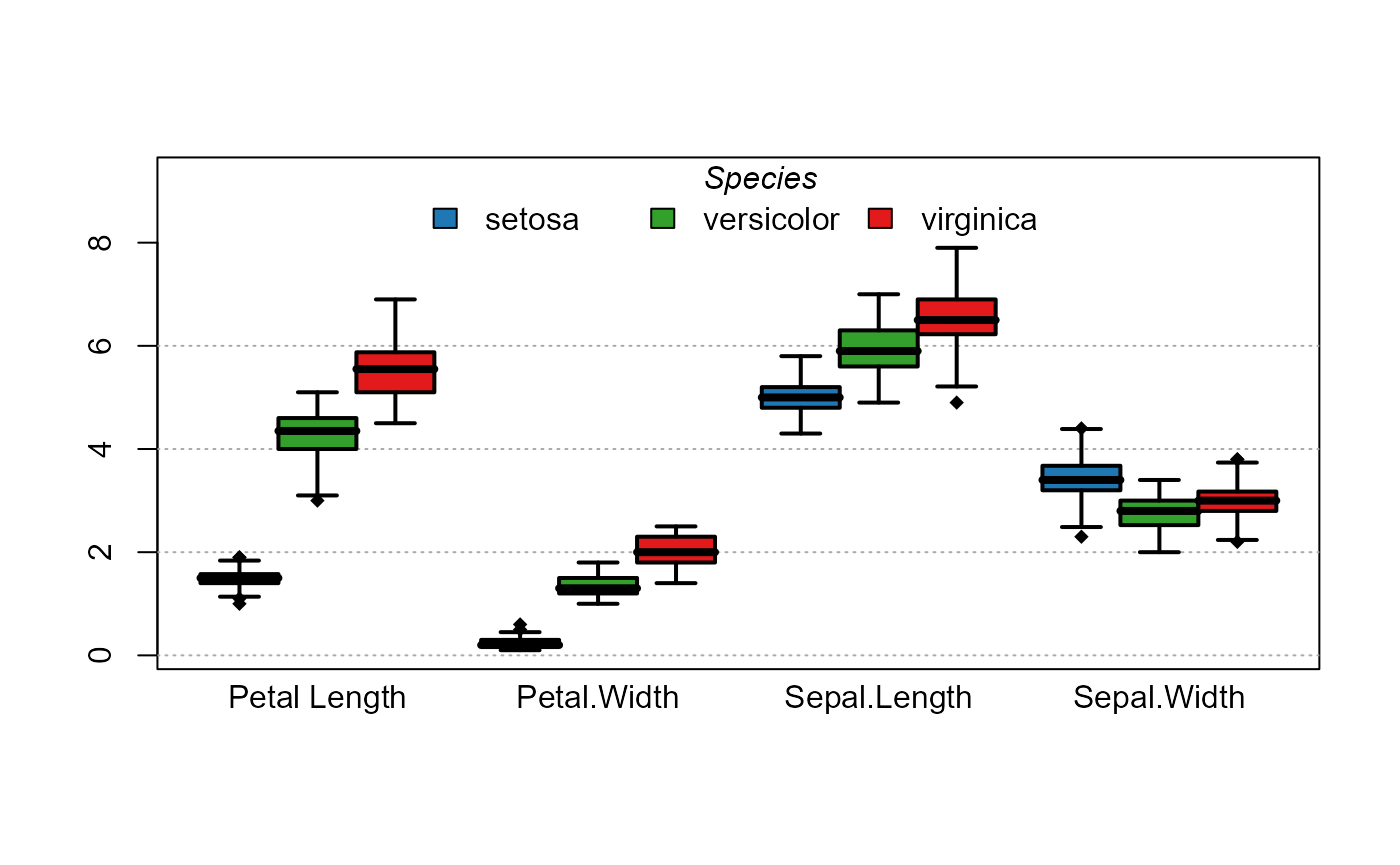

References

On the Microsoft Academic Graph data:

Arnab Sinha, Zhihong Shen, Yang Song, Hao Ma, Darrin Eide, Bo-June (Paul) Hsu, and Kuansan Wang. 2015. An Overview of Microsoft Academic Service (MAS) and Applications. In Proceedings of the 24th International Conference on World Wide Web (WWW 15 Companion). ACM, New York, NY, USA, 243-246. DOI=http://dx.doi.org/10.1145/2740908.2742839

Laurent Berge

2023-08-24